
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЛЕКЦИЯ №5
|
|
|
|
ОЦЕНКА ВОЗМОЖНЫХ ПОСЛЕДСТВИЙ ОШИБОК ПРИ ИСПОЛЬЗОВАНИИ СТАТИСТИЧЕСКИХ МЕТОДОВ РАСПОЗНАВАНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ОБЪЕКТА
РЕШАЮЩЕЕ ПРАВИЛО
ЛЕКЦИЯ №5
«РЕШАЮЩЕЕ ПРАВИЛО. ОЦЕНКА ВОЗМОЖНЫХ ПОСЛЕДСТВИЙ ОШИБОК ПРИ ИСПОЛЬЗОВАНИИ СТАТИСТИЧЕСКИХ МЕТОДОВ РАСПОЗНАВАНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ОБЪЕКТА»
ВРЕМЯ – 2 часа
ЦЕЛЬ ЗАНЯТИЯ:
Оценить возможные последствия ошибок при использовании статистических методов распознавания технического состояния объекта.
СОДЕРЖАНИЕ ЗАНЯТИЯ:
ВВОДНАЯ ЧАСТЬ – 5 мин.
УЧЕБНЫЕ ВОПРОСЫ:
1. РЕШАЮЩЕЕ ПРАВИЛО – 15 мин.
2. ОЦЕНКА ВОЗМОЖНЫХ ПОСЛЕДСТВИЙ ОШИБОК ПРИ ИСПОЛЬЗОВАНИИ СТАТИСТИЧЕСКИХ МЕТОДОВ РАСПОЗНАВАНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ОБЪЕКТА – 50 мин.
ЗАКЛЮЧЕНИЕ – 5 мин.
Правило, в соответствии с которым принимается решение о диагнозе, называется решающим правилом.
В методе Байеса объект с комплексом признаков К* относится к диагнозу, имеющему наибольшую вероятность. Это условие записывается в виде:
К* Є Di если Р (Di /К*) > Р(Dj/К*) при i ≠ j.
Условие указывает, что объект, обладающий данной реализацией комплекса признаков К *, принадлежит диагнозу (состоянию) Di. Данное правило уточняется введением порогового значения для вероятности диагноза:
Р(Di /К*) ≥ Рi,
где - Рi выбранное пороговое значение наименьшей вероятности диагноза Di.
Обычно принимается Рi ≥ 0,9. При этом вероятность ближайшего конкурирующего диагноза Рj не выше 1- Рi:
Рj < 1 - Рi = 1 – 0,9 = 0,1.
Если Р(Di /К*) < Рi, то решение о наличии у объекта диагноза Di не принимается. В этом случае для принятия решения о диагнозе требуется дополнительная информация.
При использовании статистических методов распознавания технического состояния объекта важным условием является оценка возможных последствий ошибочного диагноза. Для снижения вероятности постановки неверного диагноза необходимо правильно выбрать решающее правило. В данном случае решающее правило выбирается исходя из условия минимального риска постановки неверного диагноза.
Пример. Определить возможность постановки диагноза при использовании для распознавания технического состояния трансформатора одного признака – газа, выделяющегося из трансформаторного масла (признак → критерий → показатель → параметр).
Диагностический показатель обозначим как k. Необходимо выбрать величину параметра k0 таким образом, что бы:
- при выполнении условия k < k0 можно было бы считать трансформатор исправным и продолжать его эксплуатацию;
- при выполнении условия k = k0 принимать решение о достижении трансформатором предельного состояния;
- при выполнении условия k > k0 принимать решение о неисправном состоянии трансформатора и прекращении его эксплуатации.
Условию k < k0 соответствует работоспособное состояние трансформатора. В этом случае объекту ставится диагноз D1.
При выполнении условия k = k0 трансформатор переходит в предельное состояние и его дальнейшая эксплуатация невозможна или нецелесообразна. Этому состоянию соответствует диагноз неработоспособного состояния D2.
Условию k1 > k0 соответствует не работоспособное состояние трансформатора. В этом случае объекту ставится диагноз D2.
Таким образом, нами проведено разделение диагнозов состояния трансформатора на два класса: D1 - работоспособное состояние; D2 – неработоспособное состояние (отказ).
С учетом выбранных нами обозначений решающее правило принимает вид:
при k < k0; k Є D1;
при k ≥ k0; k Є D2.
Выделение газа неоднозначно характеризует состояние масляного трансформатора. Масло имеет собственный запах, а следовательно из него выделяется газ. В работоспособном состоянии трансформатора содержание газов не превышает допустимых пределов.
Плотность распределения функции условной вероятности показателя k для работоспособных и неработоспособных трансформаторов показана на рисунке 1.
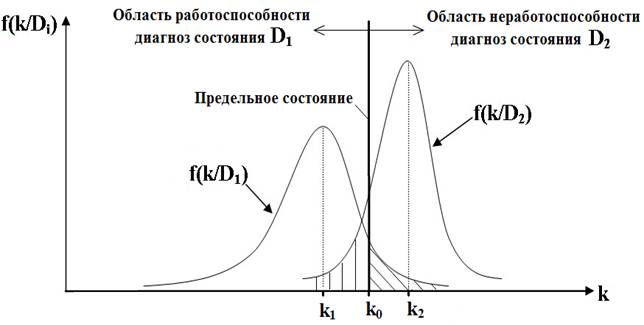
Рисунок 1. Плотность распределения функции условной вероятности показателя k для работоспособных и неработоспособных трансформаторов: f(k/D1) – функция условной вероятности появления признака k при диагнозе D1; k1 – значение показателя, при котором f(k/D1) = max; f(k/D2) – функция условной вероятности появления признака k при диагнозе D2; k2 – значение показателя, при котором f(k/D2) = max; k0 - значение параметра, при котором трансформатор переходит в предельное состояние.
Как видно из рисунка 1, функции f(k/D1) и f(k/D2) пересекаются. Справа и слева от линии предельного состояния объекта, характеризующейся условием k = k0, имеют место заштрихованные области. Наличие этих областей свидетельствует о том, что:
- трансформатор может находиться в неработоспособном состоянии при условии k < k0;
- трансформатор может находиться в работоспособном состоянии при условии k > k0.
Из данного факта можно сделать вывод, что вблизи значения k0 существует некоторая область значений показателя k, при которых трансформатор может находиться как в работоспособном, так и в не работоспособном состояниях. Поскольку реальный объект не может одновременно быть работоспособным и неработоспособным, то наличие заштрихованных областей справа и слева от значения k0 означает, что в этих областях велика вероятность постановки ошибочных диагнозов. При этом с достаточно высокой вероятностью исправный трансформатор может быть признан неисправным, а неисправный трансформатор может быть признан исправным.
Если исправному объекту вместо диагноза D1 ставят диагноз D2, то это ошибка принятия решения о диагнозе первого рода – ложная тревога.
Если не исправному объекту вместо диагноза D2 ставят диагноз D1, то это ошибка принятия решения о диагнозе второго рода – пропуск отказа.
Обозначим неверный диагноз как Dij, где i - соответствует индексу принятого диагноза, а j - индексу действительного состояния. Тогда диагноз D21 - это ошибка принятия решения о диагнозе первого рода или ложная тревога, а диагноз D12 – ошибка принятия решения о диагнозе второго рода или пропуск отказа.
Вероятность ложной тревоги Р(D21) равна вероятности произведения вероятностей двух событий: вероятности работоспособного состояния трансформатора Р(D1) и условной вероятности Р(k > k0/D1) работоспособного состояния трансформатора при условии k > k0.
Вероятность работоспособного состояния трансформатора определяется как априорная вероятность этого состояния и обозначается как Р1:
Р(D1) = Р1.
Условная вероятности Р(k > k0/D1) работоспособного состояния трансформатора при условии k > k0 определяется как интеграл функции f(k/D1) на интервале от k0 до ∞:
Р(k > k0/D1) = 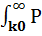 (k /D1)dk.
(k /D1)dk.
Тогда:
Р(D21) = Р1 ·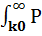 (k /D1)dk.
(k /D1)dk.
Вероятность пропуска отказа Р(D12) равна вероятности произведения вероятностей двух событий: вероятности не работоспособного состояния трансформатора Р(D2) и условной вероятности Р(k > k0/D2) не работоспособного состояния трансформатора при условии k > k0.
Вероятность не работоспособного состояния трансформатора определяется как априорная вероятность этого состояния и обозначается как Р2:
Р(D2) = Р2.
Условная вероятности Р(k > k0/D2) работоспособного состояния трансформатора при условии k > k0 определяется как интеграл функции f(k/D2) на интервале от k0 до ∞:
Р(k > k0/D2) = 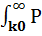 (k /D2)dk.
(k /D2)dk.
Тогда: Р(D12) = Р2 ·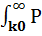 (k /D2)·dk.
(k /D2)·dk.
На практике возможны два случая постановки неправильного диагноза состояния трансформатора – ложная тревога и пропуск отказа. Это означает что суммарная вероятность Р∑(Dij) постановки неправильного диагноза равна сумме вероятностей Р(D21) ложной тревогии Р(D12) пропуска отказа:
Р∑(Dij) = Р(D21) + Р(D12) = Р1 ·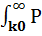 (k /D1)dk + Р2 ·
(k /D1)dk + Р2 ·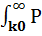 (k /D2)·dk.
(k /D2)·dk.
Данное выражение свидетельствует о достаточно высокой вероятности постановки трансформатору неправильного диагноза. Для уменьшения вероятности постановки неправильного диагноза необходимо сократить области пересечения кривых. Этого можно добиться при повышения точности измерения показателя k, а также путем более тщательного и точного определения параметра k0.
Определим возможные последствия неправильной постановки диагноза в виде величины риска R. Для этого стоимость ложной тревоги обозначим как С21, а стоимость пропуска отказа обозначим как С12. В соответствии с полученными результатами для суммарной вероятности постановки неправильного диагноза получим выражение для определения риска потерь из-за неправильного диагноза R:
R = С21·Р(D21) + С12·Р(D12) = С21·Р1 ·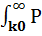 (k /D1)dk + С12·Р2 ·
(k /D1)dk + С12·Р2 ·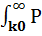 (k /D2)·dk.
(k /D2)·dk.
ЛИТЕРАТУРА:
1. Надежность и диагностика систем электроснабжения железных дорог: Учебник для вузов ж/д транспорта/ А.В. Ефимов, А.Г. Галкин. – М.: УМК МПС России, 2000.
«РЕШАЮЩЕЕ ПРАВИЛО. ОЦЕНКА ВОЗМОЖНЫХ ПОСЛЕДСТВИЙ ОШИБОК ПРИ ИСПОЛЬЗОВАНИИ СТАТИСТИЧЕСКИХ МЕТОДОВ РАСПОЗНАВАНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ОБЪЕКТА»
ВРЕМЯ – 2 часа
ЦЕЛЬ ЗАНЯТИЯ:
Оценить возможные последствия ошибок при использовании статистических методов распознавания технического состояния объекта.
СОДЕРЖАНИЕ ЗАНЯТИЯ:
ВВОДНАЯ ЧАСТЬ – 5 мин.
УЧЕБНЫЕ ВОПРОСЫ:
1. РЕШАЮЩЕЕ ПРАВИЛО – 15 мин.
2. ОЦЕНКА ВОЗМОЖНЫХ ПОСЛЕДСТВИЙ ОШИБОК ПРИ ИСПОЛЬЗОВАНИИ СТАТИСТИЧЕСКИХ МЕТОДОВ РАСПОЗНАВАНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ОБЪЕКТА – 50 мин.
ЗАКЛЮЧЕНИЕ – 5 мин.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 409; Нарушение авторских прав?; Мы поможем в написании вашей работы!