Метод наибольшего правдоподобия

ПРИМЕР

При условиях предыдущей задачи принимаем, что весовой коэффициент стоимости ложной тревоги и весовой коэффициент стоимости пропуска отказа одинаковы, т.е. С₂₁ = С₁₂. Как изменится результат диагностирования состояния опоры?

Решение:

Выражение для определения значения параметра минимального риска k_min имеет вид:

k_min = 0,5 ·(k₂ – k₁) – σ²/(k₂ – k₁)·ln(Р₂/Р₁).

Определим величину 0,5·(k₂ – k₁):

0,5·(k₂ – k₁) = 0,5·(1,6 – 1,0) = 0,3.

Определим величину σ²/(k₂ – k₁):

σ²/(k₂ – k₁) = 0,2²/(0,6) = 0,067.

Определим величину ln(Р₂/Р₁):

ln(Р₂/Р₁) = ln( 0,00001/0,99999 ) = ln( 0,00001 ) = -11,51.

Определим величину σ²/(k₂ – k₁) · )·ln(Р₂/Р₁):

σ²/(k₂ – k₁) · )·[ln(Р₂/Р₁) - ln(С₁₂/C₂₁)] = 0,067 - 11,51 = -0,77

Определим величину k_min:

k_min = 0,3 –(- 0,77) = 1,07.

Сравниваем фактическое текущее значение показателя k = 1,0 с полученной в результате расчета величиной k_min = 1,07. 1,0 < 1,07. Выполняется условие k < k_min. При k < k_min принимаем решение о том, что k 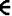D_1. Опора исправна.

Частным случаем рассмотренного метода минимального риска является метод наибольшего правдоподобия.

Правило решения по методу наибольшего правдоподобия имеет вид:

k 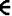D₁ при f(k/D₁)/f(k/D₂) > 1;

k 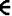D₂ при f(k/D₁)/f(k/D₂) < 1.

Выполнение условия f(k/D₁)/f(k/D₂) > 1означает, что

f(k/D₁) > f(k/D₂).

Выполнение условия f(k/D₁)/f(k/D₂) < 1означает, что

f(k/D₁) < f(k/D₂).

Проверим, как изменится результат диагностирования состояния опоры при условии предыдущей задачи.

Запишем выражения для определения значений функций f(k/D₁) и f(k/D₂):

_{2 2}

f(k/D₁) = 1/(σ )·е^{-(k – k1) /(2σ)};

_{2 2}

f(k/D₂) = 1/(σ )·е^{-(k – k2) /(2σ)}.

Введем обозначения:

_{2 2 2 2}

а = 1 /(σ ); b = е^{-(k – k1) /(2σ)}; c = е^{-(k – k2) /(2σ)}.

Тогда:

f(k/D₁) = а· b; f(k/D₂) = а· с.

а = 1/(0,2·(2·3,14) ^0,5 = 2,0; b = е^-0 = 1; с = е^-2,25 = 0,105;

f(k/D₁) = а· b = 2,0·1= 2;

f(k/D₂) = а· с = 2,0·0,105 = 0,21.

2,0 > 0,21. Выполняется условие f(k/D₁) > f(k/D₂). Принимаем решение о том, что k 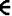D_1. Опора исправна.

Проведя диагностику состояния опоры методами минимального риска, минимального числа ошибочных решений и наибольшего правдоподобия мы получили один и тот же результат – опора исправна.

Дата добавления: 2014-01-15