Энтропия объекта с непрерывным пространством состояний

Рассмотрим некоторый объект, состояние которого характеризуется некоторым параметром х с нормальной плотностью распределения параметра, характеризуемой функцией f(х) (рисунок 1).

Для нормального распределения функции f(х) справедливо выражение:

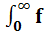(х)·dx = 1.

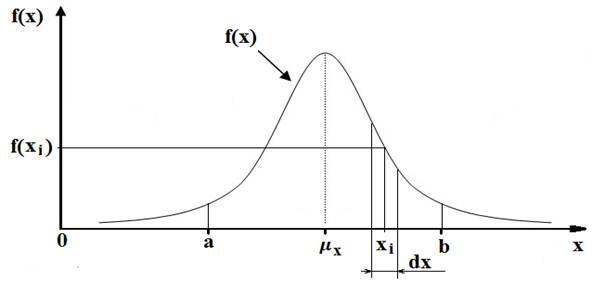
Рисунок 1. Нормальное распределение функции плотности вероятности f(х) объекта с непрерывным пространством состояний:
𝛍_х - математическое ожидание параметра х; х_i - текущее значение параметра х; f(х)_i - текущее значение функции плотности вероятности f(х)

На практике, можно выбрать такой интервал [а;b] на оси х, на котором площадь под кривой f(х) будет близка к 1, т.е.: 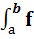(х)·dx ≈ 1.

Если рассмотреть значение функции f(х)_i на некотором интервале dx вблизи значения х_i, то можно записать: P(х_i) = f(х)_i · dx.

Это означает, что при нормальном распределении функции f(х) вероятность нахождения параметра х_i в интервале dx составляет величину P(х_i). Если разбить интервал [а;b] на n отрезков величиной dx, то получим выражение для определения величины энтропии состояний такого объекта в виде: Н = 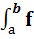(х)·log₂[f(х)]dx - log₂dx.

В случае нормального распределения Гаусса энтропия состояний объекта с непрерывным пространством состояний может быть определена по формуле:

Н = log₂[σ 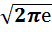/dx].

Например, при шаге квантования dx = 0,01 и параметре рассеяния σ = 0,1 получим: Н = log₂[ 0,1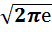 / 0,01 ] = 5,37 бит.

ЛИТЕРАТУРА:

1. Надежность и диагностика систем электроснабжения железных дорог: Учебник для вузов ж/д транспорта/ А.В. Ефимов, А.Г. Галкин. – М.: УМК МПС России, 2000, с. 298 … 302.

Дата добавления: 2014-01-15