Представлення періодичних сигналів рядом Фур’є. Пряме та обернене перетворення Фур’є

Л і т е р а т у р а

Навчальні питання

Обговорено та ухвалено

ТЕМА 5. Методи аналізу електричних кіл при не синусоїдальних напругах та струмах.

ЛЕКЦІЯ № 16

з навчальної дисципліни

“Теорія електричних та магнітних кіл”

ЗАНЯТТЯ 1. Методи розрахунків електричних кіл при не синусоїдальних напругах та струмах

на засіданні кафедри № 5.

Протокол № ______

від “____” _________2007 р.

Навчальна мета: закріпити та поглибити знання курсантів з фізичних процесів, що відбуваються в електричних колах при не синусоїдальних напругах та дії струмів із взаємною індуктивністю; прищепити практичні навички розрахунку лінійних кіл при дії не синусоїдальних напруг.

Виховна мета: виховувати та розвивати логічне мислення, самостійність, активність та ініціативу під час розв’язання задач аналізу отриманих результатів, уміння використовувати отримані знання у майбутній спеціальності.

1. Представлення періодичних сигналів рядом Фур’є. Пряме та обернене перетворення Фур’є.

2. Спектр періодичної послідовності відеоімпульсів.

3. Спектр одиночного відеоімпульсу.

4. Діюче значення та потужність в колах несинусоїдального струму.

5. Загальні відомості про спектральний метод аналізу кіл.

6. Зв‘язок між спектрами сигналів на вході та на виході кола:

а) розрахунок проходження сигналів з дискретним спектром крізь коло;

б) розрахунок проходження сигналів з суцільним спектром.

Час – 2 години

Матеріальне забезпечення:

1. Демонстраційна установка.

2. Технічні засоби навчання.

1. Каплянський А.Е. Теоретичекие основы электротехники. – М.: Москва, 1972, с.200...206.

2. Карташов Р.П., Медведев А.П. Теория елeктрорадиоцепей./Под ред.А.М.Широкова – Воениздат, 1980, с.292...349.

3. Атабеков Г.И. Основы теории цепей. М.:Энергия, 1969, с.165...177.

7. Далсонов М.В. Теорія кіл та станів. ЖВІРЕ, 1988, с.180...186.

Розрахунок та аналіз електричних кіл, як відомо, може проводитись при постійному струмові, гармонічному струмові та несинусоїдальних напругах та струмах.

В першому випадку (при постійному струмові), як відомо, використовуються закони Ома та Кірхгофа і вибирається найбільш доцільний метод розрахунку (рівняння Кірхгофа, контурних струмів, вузлових потенціалів тощо).

У другому випадку використовують метод комплексних амплітуд і аналогічні методи розрахунків.

У третьому випадку. який є найбільш поширеним на практиці, використовують спектральний метод аналізу.

Перед розглядом цього методу введемо поняття спектра.

Спектр – це сукупність усіх значень деякої фізичної величини, що повністю характеризує речовину, об’єкт, процес, явище. синтез, подію тощо.

Спектр електричного аналізу (напруги або струму) – це сукупність сигналів (напруг або струмів) заданої форми, які в сукупності утворюють початковий сигнал.

Такі складові початкового сигналу називають спектральними складовими, електромагнітними сигналами або базисом розкладу розкладу.

Відповідно розрізняють дискретні. неперервні та змішані спектри.

Дискретний спектр характеризується лічильною, а неперервний нелічильною множиною нескінченої або обмеженої кількості спектральних складових.

Змішаний спектр – це об’єднання дискретного та змішаного.

Процеси, які тривають в часі та просторі нескінченно довго, зокрема періодичні, зображаються дискретними спектрами, тобто у вигляді лічильного ряду

,

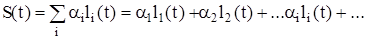де 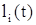- спектральні складові;

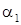- спектральні параметри.

Для неперіодичних сигналів характерним є неперервний або змішаний спектр. При цьому сигнал подається континуальною (нелічильною) множиною елементарних сигналів

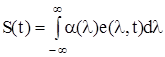
де - спектральні параметри, характеристики або функції довільного сигналу S(t).

Для аналізу електричних кіл та процесів в них при негармонічних напругах та струнах можна застосовувати різні системи елементарних сигналів (базиси).

Вибір раціонального базису розкладання для спектрального подання довільного сигналу, як правило, визначається властивостями самого аналізу та підготовленістю і придатністю до описання сигналу та процесів в колах математичного апарату.

Відповідно до цих умов в сучасній теорії і практиці найпоширенішими є ортогональні сигнали (напруги та струми).

Ортогональними називають сигнали, взаємна енергія яких на нескінченному часовому інтервалі (-¥, ¥) або його відрізку кінцевої тривалості дорівнює нулю.

Найбільш простими ортогональними сигналами є гармонічні 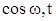та 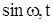однієї і тієї ж частоти, які в математичному аналізі входять як елементи узагальненого ряду 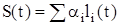, функції 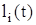і складають базис математичного аналізу. Тому для проведення спектрального аналізу періодичних сигналів використовують ряди Фур’є, елементами яких є гармонічні функції з відповідними параметрами.

Крім того, як показує практика, для заданої системи розкладання 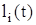та фіксованої кількості складових (членів).

Узагальнений ряд Фур’є забезпечує найкращу можливу апроксимацію (описання) довільного сигналу за критерієм середньоквадратичної похибки.

Крім рядів Фур’є та перетворень Фур’є довільні сигнали описують також системи ортогональних сигналів, які описуються поліномами Чебишева, Ерміта, Лагерра, Уолта тощо.

Зупиняються на найбільш широко представлених в базисі гармонічних функцій.

Повертаючись до функції негармонічного характеру , враховуючи, що , , а .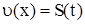

Тоді

,

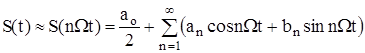де ;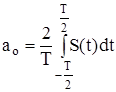

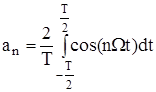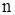, =1, 2,...;

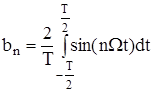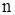, =1, 2,...

Цей розклад можна записати дещо в іншій формі

,

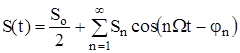в якому ; ; .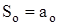

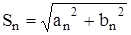Таким чином, періодичні сигнали (U або I) можна розглядати як результат накладання постійної складової і нескінченної кількості синусоїдальних коливань з частотами , , 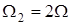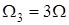з амплітудами 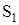, , 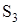і початковими фазами , , .

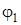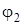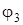Періодичними синусоїдальними струмами та напругами називають ті напруги, які змінюються в часі за періодичним несинусоїдальним законом. Вони можуть виникати при різних режимах роботи електричних кіл:

1. коли джерело ЕРС або ІДС має несинусоїдальну е.р.с. або відповідно несинусоїдальні струми, а всі елементи пасивного кола лінійні або нелінійні;

2. коли джерело ЕРС або ІДС має синусоїдальну е.р.с. або синусоїдальний струм, але один або декілька елементів кола нелінійні;

3. коли джерело ЕРС або ІДС дає постійну або синусоїдальну ЕРС, а один або декілька елементів кола періодично змінюються в часі.

Гармонічні коливання з частотами , , називають відповідно основною, або 1-ю, 2-ю та 3-ю гармоніками.

Постійна складова дорівнює середньому значенню коливання за період.

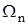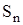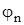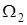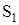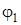
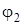Визначивши фізичний зміст коефіцієнтів , і легко перейти до можливості опису V, I послідовністю величин, які мають назви спектрів частот , ..., ,.спектрів аналізу ,.спектрів фаз. Таке представлення несинусоїдальних V та I називають спектральними.

Велике застосування на практиці значень АЧС та ФЧС, якими називають сукупності спектральних ліній, які є перпендикулярами до осі частот в точках 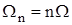, так що їх ординати дорівнюють значенням 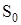, , 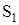, ,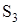...або , , .

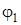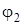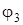Ряд Фур’є може бути представлений в комплексній формі

,

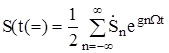де комплекс амплітуди /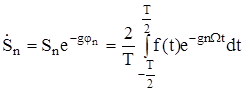

При цьому АЧС стає симетричним відносно осі ординат, ФЧС - відносно початку обліку.

За допомогою такого представлення в радіотехніці та електротехніці здійснюють перетворення періодичних сигналів, застосовуючи в подальшому до комплексних амплітуд гармонік метод комплексних амплітуд для розрахунку ЕК та відгуків ЕК на негармонійні вхідні сигнали та закони розрахунку кіл постійного струму.

Однак, якщо сигнали на вході кола є і несинусоїдальним і неперіодичним, то таке перетворення його є недопустимим. В цьому випадку забезпечують його представлення в частотній області за допомогою суми гармонік з нескінченно великим періодом слідування і нескінченно малою різницею частот за допомогою перетворення Фур’є

- пряме перетворення;

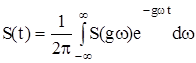- зворотне перетворення;

,

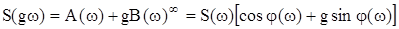де 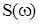- АЧС; 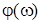- ФЧС.

Вираз (*) називають прямим перетворенням Фур¢є. Пряме перетворення Фур¢є дозволяє перейти від часової області представлення функції на комплексну щільність, а зворотне перетворення, навпаки, від комплексної щільності на часову. Перетворення фур¢є мають силу, якщо неперіодичний сигнал можна описати абсолютно інтегруємою функцією S(t), яка задовольняє умовам Дірихле (а саме: функція обмежена та має кінцеве число екстремальних значень).

На практиці іноді здається складним обчислювання спектральної щільності деяких сигналів. Розрахунок спектральної щільності значно спрощується при використанні основних теорем про сигнали та спектри.

1. Теорема лінійності.

.

2. Теорема зміщення.

.

3. Теорема запізнення

.

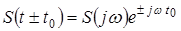4. 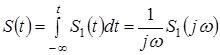- інтегрування.

5. S(t) = S(jω)

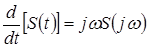- диференціювання.

Ці теореми дозволяють значно спростити розрахунок спектральних щільностей, затриманих у часі та зміщених за частотою сигналів, які ми будемо використову-вати далі.

Отже для визначення АЧС та ФЧС сигналів використовують тригонометричні перетворення для сигналів з АМ та КМ ряди Фур’є для періодичних сигналів інтеграли Фур’є для одиночних та неперіодичних сигналів.

Дата добавления: 2014-01-15