КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поведение гировертикали при маневрировании объекта
|
|
|
|
СТОИМОСТЬтранспортного обслуживания: 1150 руб.
|
ДОПОЛНИТЕЛЬНО ОПЛАЧИВАЮТСЯ ВХОДНЫЕ БИЛЕТЫ (стоимость может меняться без предварительного уведомления):
ü крепость Olavinlinna: €8, дети 7-17 лет – €4, семейный билет (2 взр.+2 реб.) – €18
ü музей леса Lusto: €10, дети 4-15 лет – €5, семейный билет (2 взр.+2 реб.) – €25
ü аквапарк Kesämaa: €18, семейный билет (2 взр.+2 реб.) – €59
ü бассейн Pikku saimaa: €6,30 учащиеся - €3,60, дети 3-6 лет – €1,20
Рассмотрим принцип действия ГВ на неподвижном основании. Предположим, что вектор 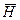 отклонен от вертикали в продольной плоскости на угол
отклонен от вертикали в продольной плоскости на угол 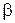 .
.
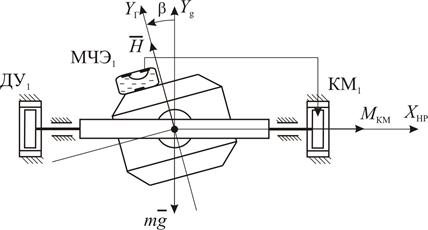 Ось
Ось 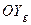 - направлена по оси местной вертикали.
- направлена по оси местной вертикали.
Ось 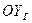 - связана с гироузлом. Она отклонена в продольной плоскости на угол
- связана с гироузлом. Она отклонена в продольной плоскости на угол 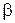 .
.
Угол 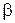 фиксируется с помощью МЧЭ1 – (маятникового чувствительного элемента), который может быть трех типов:
фиксируется с помощью МЧЭ1 – (маятникового чувствительного элемента), который может быть трех типов:
ДЖМ – датчик жидкостный маятниковый. Однокоординатный маятниковый чувствительный элемент. Включается в схему управления КМ без усилителя.
ЖМП – жидкостный маятниковый переключатель. Двухкоординатный маятниковый чувствительный элемент. Измеряет угол отклонения по двум взаимно перпендикулярным осям. Включается в схему управления КМ без усилителя.
Акселерометр – включается в схему управления КМ усилителем. Применяется в прецизионных курсовертикалях.
Примем в схеме за МЧЭ ДЖМ, так как он может быть включен в цепь управления без усилителя. Сигнал с него поступает на коррекционный мотор КМ1, который так же может быть представлен следующими типами конструкций:
- двухфазный индукционный двигатель с короткозамкнутым ротором в плоском исполнении (для удобства монтажа)
- различные типы датчиков момента.
Пусть 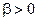 . Тогда в соответствии с правилом прецессии момент, создаваемый КМ1, направлен по оси
. Тогда в соответствии с правилом прецессии момент, создаваемый КМ1, направлен по оси 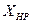 в положительном направлении.
в положительном направлении.
Аналогично рассматривается принцип действия поперечной коррекции (для 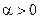 или
или 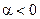 ). Его надо рассмотреть самостоятельно, составив схему аналогичную рис.1.
). Его надо рассмотреть самостоятельно, составив схему аналогичную рис.1.
Прецессионные уравнения движения гировертикали и их анализ
Прецессионные уравнения движения гировертикали могут быть составлены для следующих случаев:
1) основание, на котором установлен ГВ, неподвижно (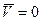 );
);
2) основание движется с постоянной скоростью (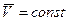 );
);
3) основание вращается с постоянной угловой скоростью (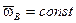 ,
,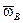 - угловая скорость виража);
- угловая скорость виража);
4) основание движется поступательно, с постоянным ускорением (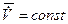 );
);
5) основание совершает сложное движение (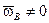 ,
, 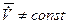 );
);
Составим обобщенное уравнение ГВ с учетом маневрирования объекта (случай 5).
Сделаем некоторые допущения:
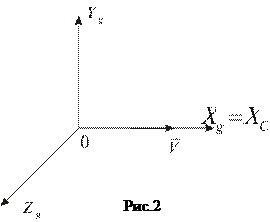 1) Касается системы координат, в которой рассматриваем движение гировертикали. В качестве системы координат выбираем скоростную горизонтальную систему координат (рис.2). Ось
1) Касается системы координат, в которой рассматриваем движение гировертикали. В качестве системы координат выбираем скоростную горизонтальную систему координат (рис.2). Ось 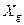 направлена по вектору путевой скорости
направлена по вектору путевой скорости 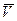 летательного аппарата, то есть принимаем, что у летательного аппарата нет угла тангажа.
летательного аппарата, то есть принимаем, что у летательного аппарата нет угла тангажа.
2) Летательный аппарат летит горизонтально, его продольная ось – горизонтальна, вектор скорости также горизонтален.
3) Углы отклонения вектора 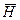 от горизонтальной системы координат (то есть от оси
от горизонтальной системы координат (то есть от оси 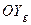 ) малы и составляют единицы градусов.
) малы и составляют единицы градусов.
4) Составляем только прецессионные уравнения, так как амплитуда нутационных колебаний очень мала и нет необходимости составлять более сложную математическую модель.
Для составления прецессионных уравнений изобразим скоростную систему координат с отклоненным по двум углам гироскопом (рис.3):
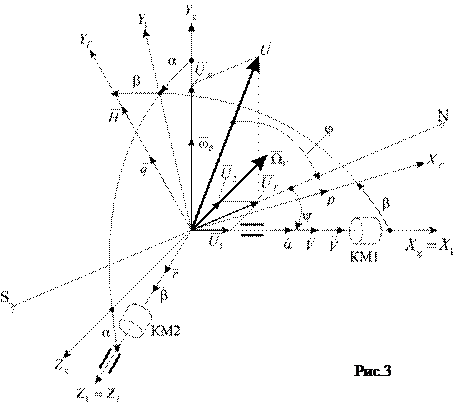
NS – след географического меридиана (полуденная линия);
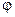 - широта места;
- широта места;
 - угол курса самолета;
- угол курса самолета;
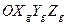 - система координат, связанная с Землей, которая совпадает со скоростной системой координат в силу принятых допущений;
- система координат, связанная с Землей, которая совпадает со скоростной системой координат в силу принятых допущений;
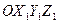 - система координат, связанная с наружной рамкой гироскопа;
- система координат, связанная с наружной рамкой гироскопа;
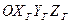 - система координат, связанная с внутренней рамкой (гирокожухом);
- система координат, связанная с внутренней рамкой (гирокожухом);
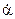 - угловая скорость вращения гироскопа вокруг оси наружной рамки
- угловая скорость вращения гироскопа вокруг оси наружной рамки 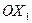 ;
;
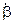 - угловая скорость вращения гироскопа вокруг оси
- угловая скорость вращения гироскопа вокруг оси 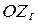 - оси подвеса внутренней рамки гиромотора;
- оси подвеса внутренней рамки гиромотора;
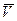 ,
, 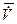 - скорость и ускорение полета самолета;
- скорость и ускорение полета самолета;
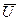 - угловая скорость суточного вращения Земли вокруг своей оси.
- угловая скорость суточного вращения Земли вокруг своей оси.
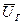 ,
,  - горизонтальная и вертикальная составляющие угловой скорости вращения Земли (проекции
- горизонтальная и вертикальная составляющие угловой скорости вращения Земли (проекции 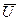 на полуденную линию NS и ось
на полуденную линию NS и ось 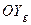 соответственно):
соответственно): 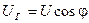 ,
,  ;
;
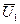 ,
, 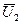 - проекции
- проекции 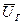 на оси координат
на оси координат 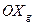 и
и 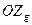 соответственно:
соответственно:
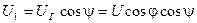 ,
,
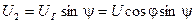
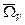 - угловая скорость облета поверхности Земли со скоростью
- угловая скорость облета поверхности Земли со скоростью 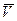 .
.
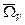 направлена по оси
направлена по оси 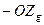 .
.
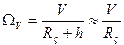 ,
,
где 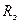 - радиус Земли,
- радиус Земли, 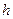 - высота полета,
- высота полета, 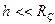 .
.
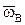 - угловая скорость разворота вокруг вертикальной оси (угловая скорость виража);
- угловая скорость разворота вокруг вертикальной оси (угловая скорость виража);
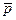 ,
, 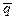 ,
, 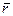 - составляющие абсолютной угловой скорости
- составляющие абсолютной угловой скорости 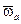 движения гировертикали по осям
движения гировертикали по осям 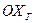 ,
, 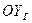 ,
, 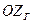 соответственно.
соответственно.
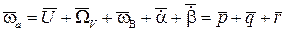 ;
;
Запишем выражения для 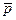 ,
, 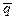 ,
, 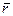 . Для этого можно использовать 2 способа:
. Для этого можно использовать 2 способа:
1) метод непосредственного геометрического проектирования.
2) метод, основанный на использовании матриц элементарных поворотов сделать САМОСТОЯТЕЛЬНО.
Используем первый способ:
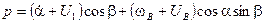 ;
;
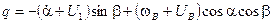 ;
;
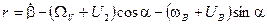 ;
;
Составляющая абсолютной угловой скорости 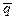 не участвует в составлении уравнений.
не участвует в составлении уравнений.
Для составления уравнений прецессионного движения гироскопа используем метод Даламбера:
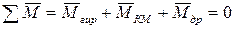 , (1)
, (1)
где 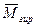 - момент, обусловленный угловой скоростью той системы координат, в которой рассматриваем движение (горизонтальной скоростной системы координат);
- момент, обусловленный угловой скоростью той системы координат, в которой рассматриваем движение (горизонтальной скоростной системы координат);
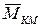 - момент коррекционного мотора;
- момент коррекционного мотора;
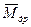 - момент дрейфа.
- момент дрейфа.
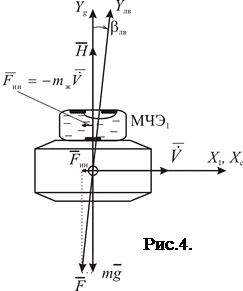 a) Спроектируем уравнение (1) на ось координат, связанную с наружной рамкой ГВ – ось
a) Спроектируем уравнение (1) на ось координат, связанную с наружной рамкой ГВ – ось 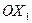 :
: 
 ; (2)
; (2)
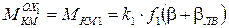 . (3)
. (3)
Поясним выражение для 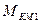 :
: 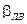 - угол ложной вертикали, возникает при действии на ГВ ускорения
- угол ложной вертикали, возникает при действии на ГВ ускорения 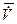 (см. рис.4);
(см. рис.4);  - сила инер-ции от ускорения
- сила инер-ции от ускорения 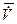 , действующая на жидкость массой
, действующая на жидкость массой 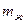 в МЧЭ1;
в МЧЭ1; 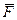 - равно-действующая
- равно-действующая  и
и 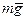 , задающая направление
, задающая направление 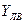 .
.

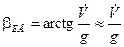
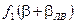 - функция от угла
- функция от угла 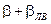 . Вид функции
. Вид функции  зависит от типа коррекции. Для случая, когда в качестве МЧЭ используется ДЖМ, функция
зависит от типа коррекции. Для случая, когда в качестве МЧЭ используется ДЖМ, функция  имеет вид, изображенный на рис.5, то есть:
имеет вид, изображенный на рис.5, то есть:
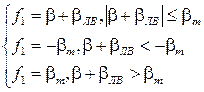
Таким образом, уравнение движения гировертикали относительно оси 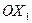 с учетом (1), (2), (3) примет вид:
с учетом (1), (2), (3) примет вид:
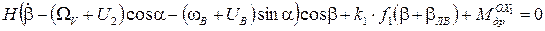 (4)
(4)
б) Составим прецессионные уравнения движения ГВ относительно оси подвеса внутренней рамки – оси 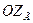 :
:
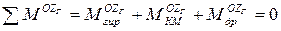 (5)
(5)
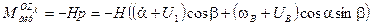 (6)
(6)
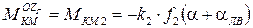 (7)
(7)
где 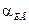 - угол ложной вертикали в поперечной плоскости. Порожден центростремительным ускорением от угловой скорости виража
- угол ложной вертикали в поперечной плоскости. Порожден центростремительным ускорением от угловой скорости виража 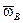 :
:
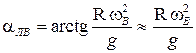 или
или 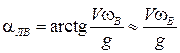 .
.
Вид функции 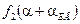 аналогичен виду функции
аналогичен виду функции 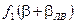 , так как в качестве МЧЭ2 так же используется ДЖМ.
, так как в качестве МЧЭ2 так же используется ДЖМ.
Таким образом, с учетом (5), (6), (7), получим следующие уравнения движения ГВ относительно оси подвеса внутренней рамки:
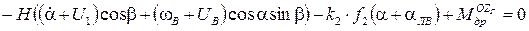 . (8)
. (8)
Примечание. Знаки коррекционных моментов выбираем из условия их включения по типу отрицательной обратной связи, т.е. чтобы вектор 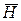 при положительных
при положительных 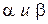 двигался к вертикали.
двигался к вертикали.
Примем следующее допущение: так как считаем углы 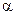 и
и 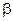 достаточно малыми, то считаем:
достаточно малыми, то считаем:
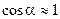 ;
; 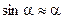 ;
; 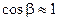 ;
; 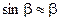 .
.
С учетом данного допущения выражения для 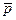 ,
, 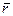 примут вид:
примут вид:
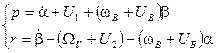 (9)
(9)
Линеаризуем уравнения (4) и (8):
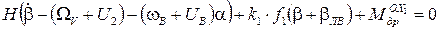 (10)
(10)
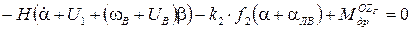 (11)
(11)
Таким образом, получены уравнения (10) и (11). Это прецессионные уравнения движения ГВ. Считая, что 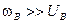 (
(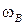 имеет порядок единиц град/сек, а
имеет порядок единиц град/сек, а 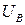 имеет порядок единиц град/час). На основе этого уравнения (10), (11) принимают вид:
имеет порядок единиц град/час). На основе этого уравнения (10), (11) принимают вид:
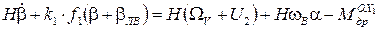 ; (12)
; (12)
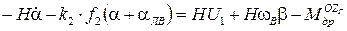 . (13)
. (13)
Уравнения (12), (13) – линеаризованные прецессионные уравнения движения ГВ для случая прямолинейного движения с маневрированием.
|
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1014; Нарушение авторских прав?; Мы поможем в написании вашей работы!