Анализ прецессионных уравнений

Решать уравнения будем путем приведения к одному уравнению.

Зададимся начальными условиями движения гирокомпаса

, .

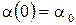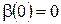Начальные условия на угловые скорости находятся в силу исходных уравнений (5), (6):

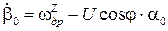
Продифференцируем уравнение (6)

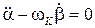(7)

Найдем зависимость от a из уравнения (5)

(8)

Подставим формулу (8) в (7)

или

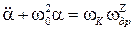, (9)

где 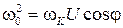- круговая частота.

Решим уравнение (9) при заданных начальных условиях

, (10)

где 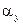- частное решение неоднородного уравнения;

.

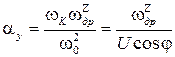Значение угла 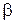находим из выражения (6)

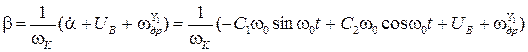. (11)

Из (10) и (11) определим константы интегрирования

;

.

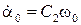Следовательно, , 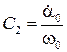и (10) и (11) приобретают вид

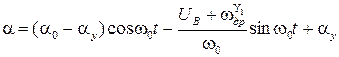; (12)

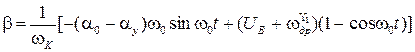. (13)

Построение фазового портрета – траектории на картинной плоскости.

Преобразуем уравнения (12) и (13).

;

,

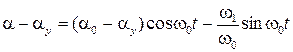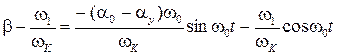где .

Или

,

где.

где .

Или

, (14)

где ; ;

.

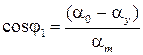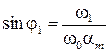, (15)

где ;

.

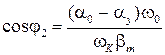
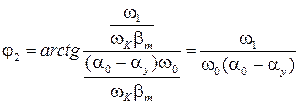Так как , то, возводя (14) и (15) в квадрат и складывая, получим

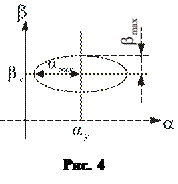Движение на картинной плоскости будет иметь вид, аналогичный изображенному на рис.4. Относительно географического меридиана ГК совершает незатухающие колебания с амплитудами, зависящими от начальных условий и параметров гирокомпаса. Причем при наличии возмущающих моментов колебания смещены относительно центра.

В реальных гирокомпасах принимаются следующие конструктивные подходы:

1) Колебания ГК должны затухать. Для этого в систему вводят специальные управляющие моменты (с помощью демпферных устройств).

2) В период запуска ГК должен приводится в меридиан автономно в течение примерно 8 часов (несколько периодов М.Шулера, мин.)

3) Периоды колебаний гирокомпаса должны удовлетворять периоду М.Шулера. Это объясняется тем, что маятниковые системы, обладающие таким периодом, обладают инвариантностью к ускорениям, то есть погрешность в определении курса не зависит от ускорений объекта.

САМОСТОЯТЕЛЬНО!

1. Рассмотреть, каким должен быть математический маятник с периодом колебаний, равным периоду М.Шулера.

2. Рассмотреть, каким должен быть физический маятник с периодом колебаний, равным периоду М.Шулера.

Дата добавления: 2014-01-15