Види випадкових величин. Дискретні випадкові величини і їх закони розподілу ймовірностей. Многокутник розподілу

Тема: Види випадкових величин. Задання випадкової дискретної величини. Повторення іспитів. Формула Бернуллі для обчислення ймовірностей

Лекція № 5

Питання лекції:

1. Види випадкових величин. Дискретні випадкові величини і їх закони розподілу ймовірностей. Многокутник розподілу.

2. Повторення дослідів. Біноміальний (біномний) закон розподілу. Формула Я. Бернуллі.

3. Найімовірніше число появи подій.

Ми вже розглянули два основні поняття теорії ймовірностей: випадкова подія і ймовірність випадкової події. Наступним важливим поняттям теорії ймовірностей є поняття випадкової величини та законів її розподілу.

Означення 1. Випадковою величиною називається величина, яка в результаті досліду може прийняти те чи інше значення, причому заздалегідь невідомо яке саме. Тобто можливі значення випадкової величини приймаються з певними ймовірностями. Випадкові величини будемо позначати через 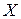, , 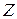і т. п., а їх можливі значення – через 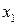, ,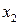..., 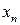і т.п. Випадкові величини бувають дискретні і неперервні.

Означення 2. Випадкова величина, можливі значення якої можна заздалегідь перелічити (перерахувати), називається дискретною випадковою величиною.

Прикладом дискретної випадкової величини може бути число відмінних оцінок в групі з 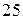студентів і т.д.

Означення 3. Випадкова величина, можливі значення якої неперервно заповнюють деякий замкнений інтервал, називається неперервною випадковою величиною.

Прикладом неперервної випадкової величини є величини напруги в мережі, вага деталі обробленої на верстаті і т.д.

Нехай дискретна випадкова величина 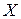приймає можливі значення 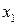, ,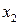..., , 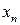тобто 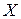може прийняти їх не достовірно, а з деякою ймовірністю. Прийняття випадковою величиною 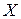якого-небудь значення 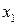, ,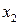..., 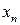будемо називати випадковою подією. Позначимо ймовірності цих подій через , ,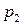..., , 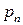що стисло записується так: 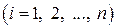, тобто 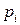є функцією від 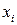. Ця функція і є законом розподілу ймовірностей випадкової величини .

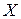Означення 4. Законом розподілу ймовірностей випадкової величини 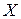називається усяке співвідношення, яке встановлює взаємозв’язок між можливими значеннями випадкової величини і відповідними їй ймовірностями.

Для дискретної випадкової величини закон розподілу задається за допомогою таблиць розподілу, де в одному рядку вказуються значення, які може приймати дана дискретна випадкова величина, а в іншому – відповідні їм ймовірності

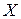
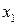
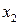
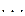
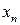
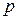
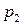
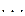
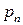
Цю таблицю часто називають рядом розподілу випадкової величини 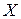. Деколи ряд розподілу відображають графічно: по осі абсцис відкладають можливі значення випадкової величини, а по осі ординат – ймовірності цих значень. Одержані точки сполучають відрізками прямих. Такий графік називається многокутником розподілу.

Зауваження. Якщо випадкова величина 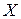може приймати тільки скінчене число різних значень 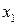, ,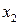..., , 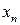то випадкові події утворюють повну групу 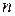несумісних подій і тоді

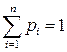. (1)

Дата добавления: 2014-01-11