
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Інтегральна теорема Маувра-Лапласа
|
|
|
|
Інтегральна теорема Маувра-Лапласа
Нехай проводяться 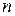 іспитів, в кожнім з яких ймовірність появи події
іспитів, в кожнім з яких ймовірність появи події 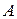 стала і дорівнює
стала і дорівнює 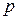
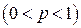 . Як розрахувати ймовірність
. Як розрахувати ймовірність 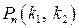 того, що подія
того, що подія 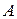 з’явиться в
з’явиться в 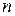 іспитах не менше
іспитах не менше 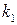 і не більше
і не більше 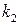 разів. Відповідь на це питання дає інтегральна теорема Маувра-Лапласа.
разів. Відповідь на це питання дає інтегральна теорема Маувра-Лапласа.
Якщо ймовірність 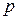 появи події
появи події 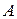 в кожнім іспиті стала і відмінна від нуля і одиниці, то ймовірність
в кожнім іспиті стала і відмінна від нуля і одиниці, то ймовірність 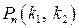 того, що подія
того, що подія 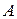 з’явиться в
з’явиться в 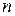 іспитах від
іспитах від 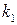 до
до 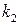 разів, приблизно дорівнює визначеному інтегралу
разів, приблизно дорівнює визначеному інтегралу
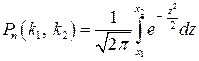 ,
,
де 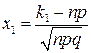 ,
, 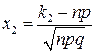 .
.
При розв’язанні задач на застосування інтегральної теореми Муавра-Лапласа, використовують спеціальні таблиці. В таблицях дані значення функції 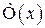 для додатних значень
для додатних значень 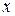 і для
і для 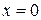 . Для
. Для 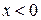 користуються тією ж таблицею.
користуються тією ж таблицею. 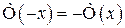 – функція непарна.
– функція непарна.
В таблиці наведені значення інтеграла до 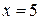 , оскільки для
, оскільки для  можна прийняти
можна прийняти 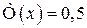 .
. 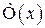 носить назву функції Лапласа.
носить назву функції Лапласа.
Формула для застосування інтегральної теореми Муавра-Лапласа отримується наступним чином:
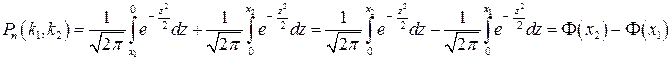 ,
,
де 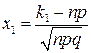 ,
, 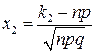 .
.
Приклад 7. Знайти ймовірність того, що з 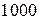 народжених буде від
народжених буде від 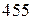 до
до 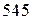 хлопчиків, якщо ймовірність народження хлопчика дорівнює
хлопчиків, якщо ймовірність народження хлопчика дорівнює 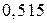 .
.
Розв’язання. Спочатку обчислимо значення 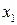 і
і 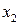 при
при 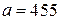 ,
, 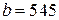 ,
, 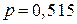 ,
, 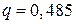 і
і 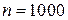 .
.
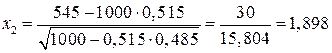 ;
;
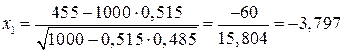 .
.
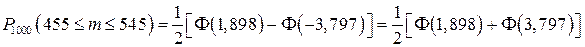 ;
;
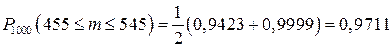 .
.
Приклад 8. Було посаджено 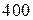 дерев. Знайти ймовірність того, що число дерев, що приживуться більше
дерев. Знайти ймовірність того, що число дерев, що приживуться більше 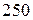 , якщо ймовірність, що окреме дерево приживеться, дорівнює
, якщо ймовірність, що окреме дерево приживеться, дорівнює  .
.
Розв’язання. Застосувавши інтегральну теорему Лапласа отримаємо
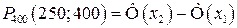
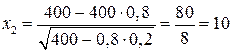 ;
;  .
.
Оскільки 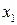 і
і 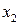 по абсолютній величині більше
по абсолютній величині більше 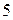 , то
, то
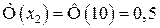 ;
; 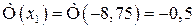 .
.
Тоді 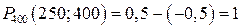 .
.
3*. Асимптотична формула Пуассона. Закон Пуассона розподілу ймовірностей рідкісних подій
Якщо ймовірність події 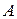 в серії
в серії 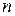 незалежних дослідів стала і дорівнює
незалежних дослідів стала і дорівнює 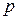 , то ймовірність того, що подія
, то ймовірність того, що подія 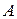 відбудеться
відбудеться 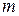 разів обчислюється за формулою Бернуллі (1), а якщо
разів обчислюється за формулою Бернуллі (1), а якщо 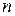 велике число, то за асимптотичною формулою теореми Муавра-Лапласа (2). Але якщо
велике число, то за асимптотичною формулою теореми Муавра-Лапласа (2). Але якщо 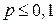 – мале число, тобто маємо справу з рідкісними подіями, а
– мале число, тобто маємо справу з рідкісними подіями, а 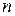 – число велике (взагалі
– число велике (взагалі 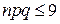 ), то формула (1), дає велику похибку. В цьому випадку ймовірність
), то формула (1), дає велику похибку. В цьому випадку ймовірність 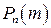 обчислюється за так званою асимптотичною формулою Пуассона.
обчислюється за так званою асимптотичною формулою Пуассона.
Зробимо при виведенні формули Пуассона одне допущення, а саме будемо вважати, що добуток 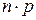 зберігає стале значення, тобто
зберігає стале значення, тобто 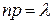 .
.
Скористаємося при виведенні формули Пуассона формулою Бернуллі:
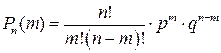
або
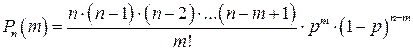
Оскільки 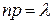 , то
, то 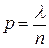 . Отже:
. Отже:
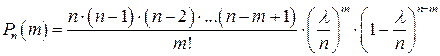
Оскільки 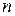 дуже велике, то будемо шукати
дуже велике, то будемо шукати 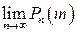 . При цьому слід замітити, що буде знайдене лише наближене значення ймовірності, в зв’язку з тим, що хоча
. При цьому слід замітити, що буде знайдене лише наближене значення ймовірності, в зв’язку з тим, що хоча 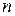 і велике, але скінчене число. Оскільки
і велике, але скінчене число. Оскільки 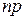 зберігає стале значення, то при
зберігає стале значення, то при 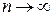 ,
, 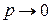 маємо
маємо
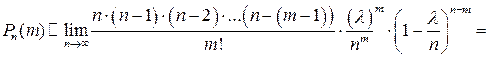
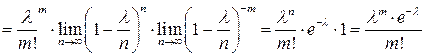 .
.
Отже, формула Пуассона
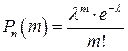 . (3)
. (3)
Вона відображує закон розподілу масових (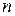 велике) і рідкісних (
велике) і рідкісних (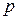 мале) подій.
мале) подій.
Якщо у формулі (3) 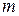 приймає цілі значення від
приймає цілі значення від 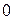 до
до 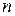 , то одержимо закон Пуассона розподілу ймовірностей рідкісних подій, який можна записати у вигляді таблиці:
, то одержимо закон Пуассона розподілу ймовірностей рідкісних подій, який можна записати у вигляді таблиці:
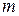
| 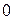
| 
| 
| 
| 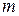
| 
| 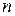
|
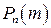
| 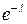
| 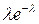
| 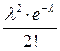
| 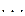
| 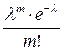
| 
| 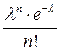
|
Для обчислення ймовірностей 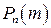 за формулою (3) також є таблиці. Формула (3) є достатньо точною починаючи з
за формулою (3) також є таблиці. Формула (3) є достатньо точною починаючи з 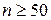 .
.
Приклад 9. В коробці лежать 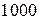 резисторів, десять з яких непридатні. Обчислити ймовірність того, що серед
резисторів, десять з яких непридатні. Обчислити ймовірність того, що серед 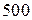 взятих навмання резисторів три з них будуть непридатними.
взятих навмання резисторів три з них будуть непридатними.
Розв’язання. За класичною формулою обчислюємо 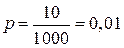 ,
, 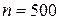 , тоді
, тоді 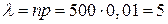 ,
, 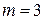 . За формулою (3) маємо,
. За формулою (3) маємо,
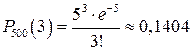 .
.
Приклад 10. Комутатор установи обслуговує 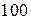 абонентів. Ймовірність того, що на протязі
абонентів. Ймовірність того, що на протязі 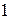 хв. Абонент подзвонить на комутатор, дорівнює
хв. Абонент подзвонить на комутатор, дорівнює 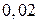 . Яка з двох подій ймовірніше: на протязі
. Яка з двох подій ймовірніше: на протязі 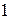 хв. подзвонить
хв. подзвонить 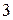 абоненти або подзвонить
абоненти або подзвонить 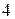 абоненти.
абоненти.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1039; Нарушение авторских прав?; Мы поможем в написании вашей работы!