Традиционные КК Шухарта

8.5.1 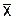-карта контроля Шухарта

Согласно следствию из теоремы Лиденберга-Фёллера распределение значений выборочного среднего 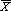случайных выборок, полученных из одной генеральной совокупности, стремится к нормальному при объеме выборки, равном или большем 4, даже если эта генеральная совокупность не является нормальной. Почти все значения (за исключением только 0.27%) в нормальном распределении лежат внутри интервала среднее ± 3-сигма.

Отсюда следует, что если в длинной последовательности измерений выборки являются нормальными и произведены из одной генеральной совокупности, то их средние почти всегда попадают внутрь интервала (m ± 3s). Это видно из рисунка 8.3, на котором изображена контрольная карта для средних 100 выборок по 4 из нормально распределённой совокупности чисел, представленных в таблице 8.2. Ни одна точка не выходит за контрольные пределы 45 и 15. Для 1000 выборок по 4 из этого резервуара только 2 из 1000 точек выходят за эти контрольные пределы.

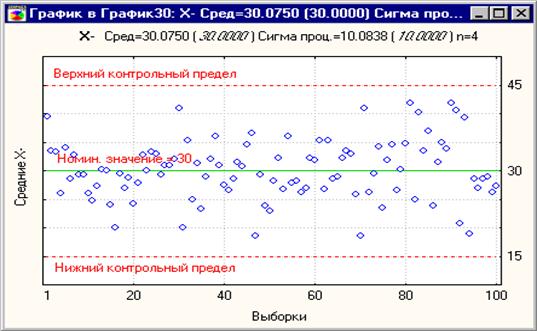
Рисунок 8.3

Таблица 8.2 - 400 измерений, объединенные в выборки по 4

Измерения	Среднее	Размах R	Стд. откл. s
				39,5		7,1
				33,5		0,6
				33,25		1,5
						14,9
						7,6
				28,5		7,5
				32,75		10,1
				29,25		12,9
				29,25		6,9
						8,8
				24,75		12,8
				27,25		9,1
				30,25		3,8
						15,4
						4,9
						13,7
				29,5		9,5
						2,9
				28,75		7,1
				24,25		7,9
				27,75		8,1
				32,75
						13,8
				33,25		8,8
						8,2
				29,25		7,6
						12,5
						3,2
						19,1
						9,9
				35,25		6,3
						9,7
				31,25		8,7
				23,25		6,7
						7,8
						20,1
						12,4
						5,4
				27,5		8,1
				26,5		11,7
				28,5		7,6
				31,5		12,5
				30,75		10,5
				34,5		8,7
				36,5		10,9
				18,5		13,3
				29,25		10,5
				23,75		5,1
				28,25		14,4
				32,25		4,6
				26,75		10,9
						2,9
				27,75
				28,25		13,5
				26,25		6,2
						14,7
				32,25		8,5
				31,75		7,3
				35,25		7,3
				26,75		8,2
				35,25		11,6
				28,5		7,9
						9,6
				32,25		9,4
				33,5		9,8
						6,7
				25,75		13,7
				18,5		8,9
						5,5
				26,25		9,1
				29,5		8,1
				34,25		6,1
				23,5		15,7
				31,75		7,2
				34,5		5,8
				26,5		6,6
				30,25		2,5
				34,75		7,1
				41,75		12,9
						4,8
				40,25		8,7
				33,5		13,1
						13,7
				23,75		6,2
				31,5
						7,4
				33,75		10,7
				41,75		15,1
				40,5
				20,75		17,3
				39,25		15,3
						8,3
				28,5
						20,5
				28,5
						11,1
				26,25		7,1
				27,25		6,1

На рисунке 8.3 центральная линия установлена в значение 30, равное m, известному значению математического ожидания генеральной совокупности. Пределы «3 - сигма» могли быть вычислены на основе известного значения s, которое округленно равно 10. Стандартная ошибка для среднего (стандартное отклонение выборочного среднего как случайной величины) равна:

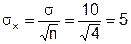
Следовательно, границы «3-сигма» расположены на расстоянии 3s=3*5=15 от значения 30, что соответствует верхнему контрольному пределу 45 и нижнему контрольному пределу 15.

Неверно утверждать, что для длинной серии, при условии неизменности генеральной совокупности, за границы 3-сигма на 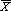-карте будут выходить именно 27 точек из 10000 (т.е. 0.27% всех наблюдений). Это может быть верным только в случае, когда значения 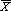в точности нормальные и контрольные пределы основаны на известных значениях m и s. На практике, несмотря на то, что распределение значений 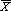приблизительно нормально, этим фактом нужно пользоваться осторожно. Если генеральная совокупность не нормальна, то границы 3-сигма предпочтительнее вычислять по наблюдаемым данным, а не по параметрам генеральной совокупности. Границы 3-сигма при неправильном применении могут стать плохими индикаторами отсутствия статистической устойчивости.

Границы 3-сигма редко дают ошибку при обнаружении нарушений в работе процесса (т.е. неслучайных причин изменчивости), когда на самом деле нарушений не происходит. Если точки на 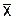-карте попадают вне границ 3-сигма, это хорошее основание для уверенности в том, что наблюдается влияние на изменчивость качества некоторых факторов, которые должны быть выявлены.

8.5.2 Вычисление границ 3-сигма для контрольных 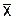-карт

Ниже будут произведены вычисления контрольных пределов для 20 первых выборок из таблицы 8.2. После вычисления средних и размахов выборок следующим шагом является вычисление 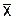и . Для первых 20 выборок вычисления дают:

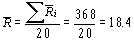
Далее оценивается s с помощью таблицы 8.6. Для этого нужно определить из таблицы 8.6 значение фактора d₂ для данного размера выборок. В нашем случае n = 4, и таблица 8.6 дает d₂ = 2,059. Тогда:

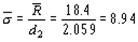
Теперь 3s можно вычислить по формуле (с учётом ):

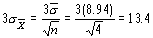
Верхний контрольный предел 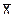= = 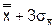28,9 + 13.4 = 43,3

Нижний контрольный предел 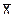= = 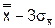28,9 – 13.4 = 15,5

Эти два шага вычисления 3s могут быть объединены в одном

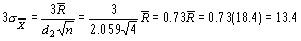
Для облегчения вычислений контрольных пределов по значения множителя для всех значений n от 2 до 20 приведены в таблице 8.7. Этот множитель обозначен как A₂. Формулы для вычисления контрольных пределов 3-сигма для 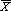-карты принимают вид:

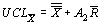
Если контрольные пределы вычисляются не по , а по , то вычисления для первых 20 выборок принимают вид:

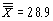
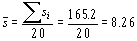
Далее используется значение c₄ из таблицы 8.6.

Оценка s, , ,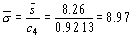

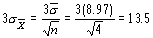где 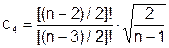, причём (1/2)!=.

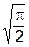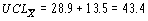
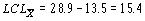
Как и при вычислении по , два шага вычисления 3s могут быть объединены в одном:

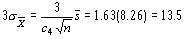
Для облегчения вычислений контрольных пределов по значения множителя 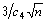для всех значений n от 2 до 25 приведены в таблице 8.8. Этот множитель обозначен как A₃. Формулы для вычисления контрольных пределов 3-сигма с использованием этого множителя принимают вид:

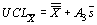
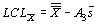
Для тех ситуаций, когда желательно вычислять контрольные пределы прямо по известным стандартным значениям s и m, множитель 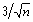вычислен и приведен в таблице 8.9. Этот множитель обозначен как A. Формулы для вычисления контрольных пределов 3-сигма с использованием этого множителя принимают вид:

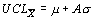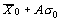
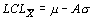или

или .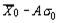

По этим формулам были вычислены контрольные пределы для контрольной карты на рисунке 8.3. В данном случае для известных значений m = 30 и s = 10 значение для A в таблице 9 равно 1.50 и

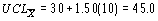
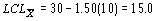
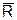Различные уравнения для центральной линии и контрольных границ 3-сигма на контрольных картах для 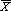, и собраны вместе в таблице 8.3. Множители (такие как A, A₁ и т.д.) берутся из таблиц, приведенных в приложении. Читатель заметит, что диапазон границ для 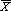-карты, так же как и для или карты, 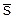зависит от дисперсии процесса. Пределы для всех карт могут быть вычислены прямо по известной или предполагаемой s путем оценки или . В промышленной практике в большинстве случаев границы вычисляются по .

Таблица 8.3 - Уравнения для вычисления контрольных пределов 3-сигма

Метод	-карта	R -карта	s -карта
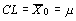
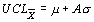
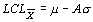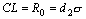
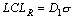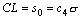
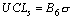
m и s известны или предполагаемы (X0, s0)	таблица 8.9	таблицы 8.6 и 8.9	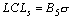таблицы 8.6 и 8.9
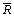
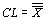
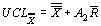
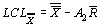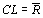
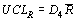
m и s оценены по и	таблица 8.7	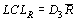таблица 8.7
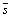
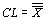
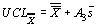
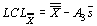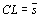
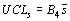
m и s оценены по и	таблица 8.8		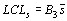таблица 8.8

Дата добавления: 2014-01-15