Звенья второго порядка

Общее уравнение:

Характеристическое уравнение

Корни уравнения

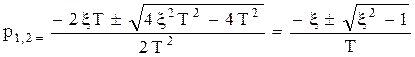
1. Если 0<ξ<1, то корни – комплексные, звено называется колебательным.

2. Если 1≤ξ, то корни действительные, звено – апериодическое 2-го порядка.

3. Если ξ=0, корни чисто мнимые – звено называется консервативное.

ξ –коэффициент демпфирования, т.е. коэффициент сглаживания пульсаций.

- передаточная функция.

VI. 1. Колебательное звено.

0<ξ<1

3.h(t)

y(t)=y_общ(t)+y_частн.(t), x=1(t), y(0)=0; y`(0)=0.

,

где , .

Общее решение в данном случае: y_общ=Сe^αtsin(βt+γ), y_ч=к1(t)

y(t)=(Сe^αtsin(βt+γ)+к)1(t)

y(0)=C sin(γ)+к=0

y`(0)=|αCe^αt sin(βt+γ)+ βСe^αtcos(βt+γ)|= αC sin(γ)+βСcos(γ)=0

, ,

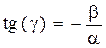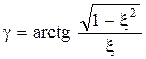
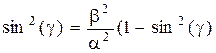
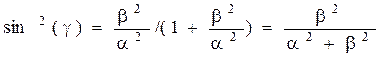
β- частота колебаний.

α-определяет скорость затухания колебаний, причем чем меньше

время T, тем быстрее затухают колебания, и чем больше ξ тем быстрее

затухают колебания

4.

t

ω(t)

5.

ImW(jω)

ReW(jω)

	k		Re

Im

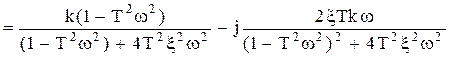
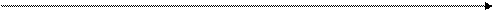
6.

Причем - будет тем больше, чем меньше ξ.

ω^* - называется резонансной частотой; коэффициент усиления на этой

частоте максимальный.

7.

		ω

-π

-π/2

8. ЛАХ

-40 дб/дек

Реальная ЛАХ

L(θ)

1/T

L_a(θ)

-20lg(k)

-20дб/дек

ω

L(θ)

θ

L(θ)=20lg(A(θ))

VII. ξ=0, консервативное звено.

, ,

3. y(t)=(Сsin(βt+γ)+k)1(t)

Из начальных условий: Csin(γ)+k=0,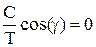

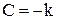
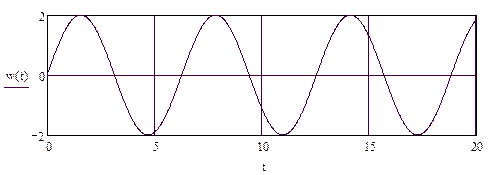
4.

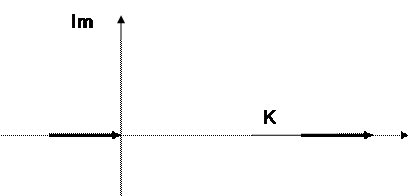
5.

	Re

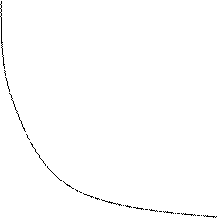
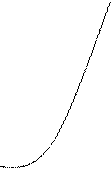6.

		1/T

7.

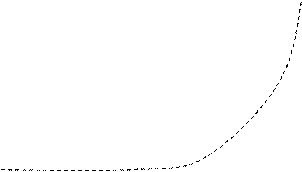8. ЛАХ

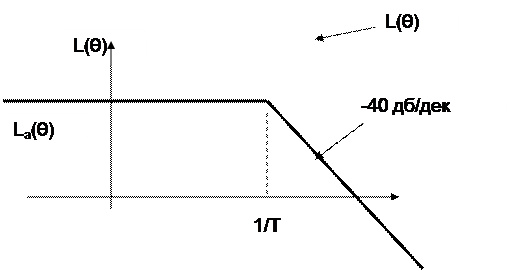
ξ≥1, апериодическое звено 2-го порядка

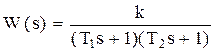, где T₁*T₂=T², T₁+ T₂=2ξT

Последовательное соединение 2-х апериодических звеньев 1-го порядка.

3. h(t)=k(C₁e^-t/T+ C₂e^-t/T+1)

K

h(t)

t

Кривая 2-го порядка имеет перегиб.

В начале производная должна быть равна 0, а за тем “+”.

t

ω(t)

4. Частотные характеристики рассматриваются далее…

IX. Неминимальнофазовые звенья

Звено первого порядка

=

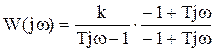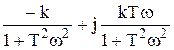
АЧХ – как у апериодического звена.

Комплексная частотная характеристика:

-K

Im

Re

		ω

-π/2

-π

X Звено транспортного запаздывания.

1. y(t)=kx(t-τ) (конвейер, труба)

2. W(S)=ke^sτ

3. h(t)=k1(t- τ)

4. ω(t)=kδ(t- τ)

5. W(jω)=k*e^-jωτ=k(cos(ωt)-jsin(ωt))

k

Re

Im

6. A(ω)=k

γ (ω)=-ωτ

ω

γ(ω)

Лекция 7

Дата добавления: 2014-01-15