Получение временных характеристик для соединения звеньев

В общем случае можно записать передаточную функцию соединения, по ней восстановить дифференциальное уравнение т решить его при соответствующих входных воздействиях и нулевых начальных условиях.

В частных случаях можно использовать свойства звеньев. Так последовательное соединения звеньев интегрирующего и дифференцирующего с апериодическим, получило название реальное дифференцирующее звено с передаточной функцией:

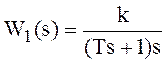
позволяет получать временные характеристики по следующим соображениям:

- если есть переходной процесс апериодического звена I-го

порядка

h(t)=k(1-e^-t/T)

то

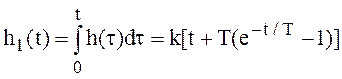
ω₁(t)=h(t)

аналогично можно сделать преобразовать для реального интегрирующего звена.

h₂(t)= ω(t)

ω₂(t)=h`₂(t)

аналогично можно получить временные характеристики при последовательном соединении интегрирующего и дифференцирующего звеньев.

Параллельное соединение. При построении временных характеристик следует воспользоваться принципом суперпозиции. В частности реальное форсирующее звено:

Данное выражение можно представить в виде соединения интегрирующего и апериодического звеньев.

h(t)= h₁(t)+h₂(t)=ω₂(t)*T₁+h₂(t)

			t

Для встречно параллельного соединения упрощение передаточных функций представляя передаточные функции в виде дробно-рациональных:

тогда

Для единичной обратной связи:

Аналогично осуществляется преобразования передаточных функций записанных в операторной форме.

Дата добавления: 2014-01-15