Поняття множини. Способи задання множини

Теорія множин є теоретичною основою не лише дискретної, а й усієї сучасної математики.

Більшу частину понять дискретної математики можна визначити за допомогою поняття множини. В понятті множини виявляється високий рівень абстракції, який притаманний математиці. Поняття множини і її елемента відносять до основних, первинних понять математики. Вважають, що ці поняття, які і будь-які інші вихідні поняття деякої математичної теорії, не визначаються.

Під множиною розуміють сукупність певних об’єктів, які об’єднані спільними властивостями. При цьому природа самих об'єктів, що становлять ту або іншу множину нас не буде цікавити. Творець теорії множин Георг Кантор давав наступне означення множини – "множина є багато чого, мислиме нами як ціле."

У повсякденному житті та практичній діяльності для позначення поняття множини використовують також слова: набір, клас, система, комплекс і т. ін. Але й у математиці термін множина має низку синонімів. Так, замість «множина значень змінної» можна сказати «область значень змінної», замість «множина кривих» – «сім’я кривих», замість «множина двох рівнянь» – «система двох рівнянь» і т. ін.

Об’єкти будь-якої природи, що утворюють множину, називаються її елементами. Наприклад, в множині студентів університету елементом буде студент, в множині днів тижня елемент – «четвер». Елементами множин можуть бути самі множини. Наприклад, множина академгруп університету, кожна академгрупа – множина студентів.

Для позначення конкретних множин використовують великі букви латинського алфавіту: або великі букви з індексами .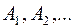

Для деяких особливо важливих числових множин прийняті стандартні позначення, яких слід дотримуватися. Так,

позначають відповідно множину натуральних чисел;

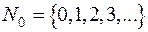– множину цілих невід’ємних чисел;

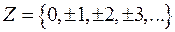– множину цілих чисел;

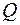– множину раціональних чисел;

– множину дійсних чисел;

– множину комплексних чисел.

Для позначення елементів множин використовують малі букви латинського алфавіту: 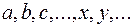або малі букви з індексами .

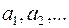Належність елемента множині позначається символом 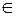: – елемент 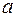належить множині (знак 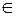є стилізацією першої букви грецького слова – бути, існувати); неналежність елемента множині позначається символом : .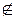

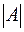Означення. Множина називається скінченною, якщо вона складається із скінченного числа елементів. Кількість елементів у скінченній множині називається потужністю множини и позначається . Множину потужності 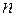(), тобто таку, яка складається з 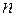елементів, часто називають ще 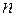-множиною. Множина, що не містить жодного елемента, називається порожньою і позначається символом . Множина, що містить всі елементи, що знаходяться в розгляді, називається універсальною або універсумом і позначається .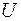

Наприклад, множина всіх мешканців на земній кулі – скінченна, а множина всіх трикутників на площині – нескінченна. Множина всіх дійсних коренів рівняння 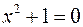порожня. Множина дійсних чисел є універсальною відносно всіх чисел, що розглядаються, наприклад, в шкільному курсі математики. Множина комплексних чисел є універсальною відносно всіх чисел, що розглядаються в математичному аналізі.

Множина вважається заданою, якщо про будь-який її елемент можна сказати, належить він цій множині чи не належить.

Дата добавления: 2014-01-11