Операції над відношеннями

Образи і прообрази елементів і множин відносно відношень.

Нехай між множинами і встановлено відношення . З кожним бінарним відношенням 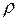на множинах і зв’язані деякі множини.

Означення. Множина називається множиною відправлення, множина називається множиною прибуття відношення.

З кожним бінарним відношенням 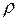на множинах і зв’язані ще дві множини – область визначення і область значень.

Означення. Множина 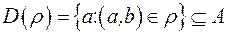перших компонент всіх пар, які входять до відношення 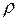називається областю визначення відношення 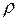. Множина 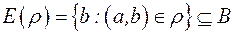других компонент всіх пар, які входять до відношення 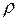називається областю значень відношення .

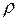Зобразимо відношення між множинами і на діаграмі Ейлера-Венна:

Приклад. Розглянемо відношення з прикладу 2, явний запис якого має вигляд:.Тоді 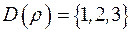, 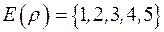. Означення. Сукупність всіх тих 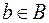, в які переходить даний елемент , називається образом елемента і позначається . Сукупність всіх тих , які переходять в даний елемент 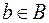, називається прообразом елемента 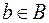і позначається 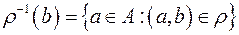. Аналогічно визначаються образ 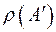множини 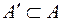і прообраз 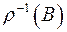множини .

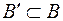Оскільки відношення – це множини, над ними можна виконувати всі теоретико-множинні операції: переріз, об’єднання, віднімання, доповнення. При цьому виконуються всі закони алгебри множин. Крім того для відношень має зміст операція обернення. Перехід від 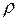до здійснюється взаємною перестановкою компонент кожної пари, яка входить до відношення.

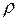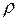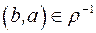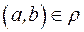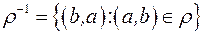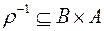Означення. Нехай – бінарне відношення на множинах і . Відношенням, оберненим до відношення називається таке відношення , що тоді і тільки тоді, коли . .Отже, якщо , то і 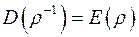, 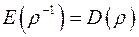. Приклад. Нехай 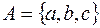і 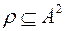: 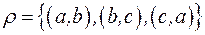. Тоді.

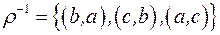Якщо два відношення і 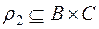застосувати послідовно, то можна знайти їх композицію, тобто побудувати нове відношення 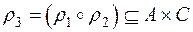, при умові, що елементи області значень першого відношення є елементами області визначення другого відношення.

Означення. Композицією двох відношень і 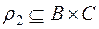називається відношення 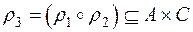, де

.

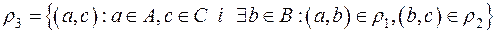Нехай , .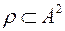

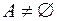Для будь-якої непорожньої множини визначимо такі окремі випадки відношень.

Означення. Повним (універсальним) відношенням називається відношення, яке виконується для будь-якої пари елементів множини .

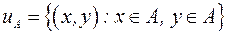Таким чином, .

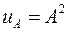Наприклад, універсальними є відношення „вчитися в одній академгрупі” на множині студентів конкретної групи.

Означення. Порожнім відношенням називається відношення, яке не виконується для жодної пари елементів множини .

Таким чином, оскільки , то є відношенням на .

Наприклад, порожнім є відношення „бути братом” на множині жінок.

Означення. Тотожним (діагональним) відношенням називається відношення, яке виконується тільки між елементом множини і ним самим.

.

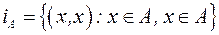Наприклад, тотожнім є відношення з прикладу 5.

Дата добавления: 2014-01-11