Приклади

1. Відношення строгої нерівності на числових множинах :

.

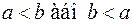2. Відношення „бути батьком” в множині людей.

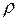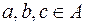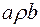Означення. Відношення називається транзитивним, якщо для будь-яких з і 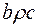випливає . ()

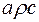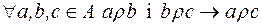Приклади. 1. Відношення =, 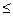, «жити в одному місті».

2. Відношення ‘‘мати непорожній переріз’’ на системі множин не є транзитивним.

Одночасне виконання умов 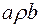, , 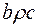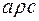означає, що пара 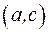належить композиції 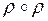. Тому для транзитивного відношення .

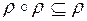Означення. Відношення 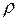називається зв’язним, якщо для будь-яких 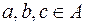з 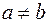випливає 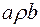або ().

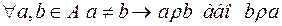Для зв’язного відношення .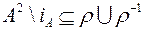

Наявність певної властивості легко прослідкувати за матрицею або за графом відношення:

Властивості спеціального бінарного відношення 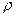, визначеного на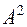

Відношення має (+), не має (-) властивість:	Властивість	Особливості матриці відношення	Особливості графа
Рефлексив - ність	+		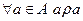Всі елементи головної діагоналі дорівнюють 1	Всі вузли мають петлі
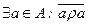
–		На головній діагоналі є хоча б один 0	Є хоча б один вузол без петлі
Антирефлексивність	+		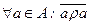Всі елементи головної діагоналі дорівнюють 0	Всі вузли не мають петель
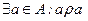
–		На головній діагоналі є хоча б одна 1	Є хоча б один вузол з петлею
Симет - ричність	+		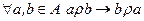Матриця симетрична відносно головної діагоналі	Для кожної дуги, що сполучає два вузли, існує також дуга, що сполучає ці вузли у зворотному напрямі
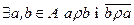
–		Матриця несиметрична	Є два вузли, сполучені тільки одній дугою
Антисимет - ричність	+		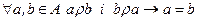В матриці нема 1, симетрично розташованих відносно головної діагоналі	Не існує двох різних вузлів, зв'язаних парою різнонапрямлених дуг
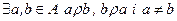
–		В матриці є хоча б дві 1, симетрично розташовані відносно головної діагоналі	Є два вузли, сполучені двома різно-напрямленими дугами
Асимет - ричність	+		В матриці нема 1, симетрично розташованих відносно головної діагоналі, всі елементи якої дорівнюють 0	Не існує двох різних вузлів, зв'язаних парою різнонапрямлених дуг
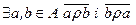
–		В матриці є хоча б дві 1, симетрично розташовані відносно головної діагоналі, або на головній діагоналі є хоча б одна 1	Є два вузли, сполучені двома різно-напрямленими дугами
Транзитив - ність	+		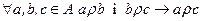	Для будь-яких двох дуг, таких, що одна напрямлена від а до b, а друга – від b до с, існує дуга, яка з’єднує а з с в напрямі від а до с.
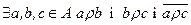
–			Існують дві дуги, такі, що одна напрямлена від а до b, а інша – від b до с, і при цьому немає дуги від а до с.

Дата добавления: 2014-01-11