Топологические модели

На уровне самого общего представления любая сеть состоит из совокупности пунктов и соединяющих их линий, взаимное расположение которых характеризует связность сети и способность к обеспечению информационного обмена между различными адресатами. Структура, отображающая расположение пунктов сети и связывающих их линий называется топологией сети. Различают физическую топологию и логическую. Физическая топология отображает размещение пунктов в пространстве и конфигурацию линий связи. Логическая топология дает представление о путях перемещения информационных сообщений в сети от источников к приемнникам на основе адресной информации.

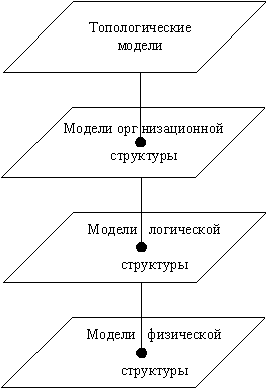Рисунок 1. Системное описание архитектуры сети

Для исследования топологических особенностей сети ее удобно изображать в виде точек и соединяющих их дуг. Такая геометрическая фигура носит название граф. Точки в графе именуются вершинами, а дуги, если не учитывается их направленность, – ребрами. Граф является моделью топологическойструктуры информационной сети. Выбор топологии является наипервейшей задачей, решаемой при построении сети. Он осуществляется с учетом таких требований, как экономичность и надежность связи. Задача выбора топологии сети решается сравнительно несложно, если известен набор типовых топологий (примитивов), которые можно использовать как отдельно, так и в комбинации. Рассмотрим ряд таких типовыхтопологий, назовем их базовыми, и охарактеризуем их особенности.

Топология «точка – точка» является наиболее простым примером базовой топологии и представляет собой сегмент сети, связывающий физически и логически два пункта (рис 2).

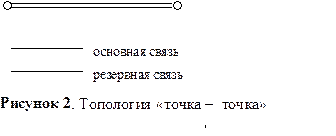
Надежность связи в таком сегменте может быть повышена за счет введения резервной связи, обеспечивающей стопроцентное резервирование,

называемое защитой типа 1+1. При выходе из строя основной связи сеть автоматически переводится на резервную. Несмотря на всю простоту, именно эта базовая топология наиболее широко используется при передаче больших потоков информации по высокоскоростным магистральным каналам, например, по трансокеанским подводным кабелям, обслуживающим цифровой телефонный трафик. Она же используется как составная часть радиально-кольцевой топологии (в качестве радиусов). Топология «точка–точка» с резервированием типа 1+1 может рассматриваться как вырожденный вариант топологии «кольцо» (см. ниже).

Древовидная топология может иметь различные варианты (рис. 3).

Рисунок 3. Древовидная топология: а – дерево, б – звезда, в – цепь

Особенностью сегмента сети, имеющего древовидную топологию любого из перечисленных вариантов, является то, что связность n пунктов на уровне физической топологии здесь достигается числом ребер R = n – 1, что обеспечивает высокую экономичность такой сети. На логическом уровне, количество связывающих путей передачи информации между каждой парой пунктов в таком сегменте всегда равно h = 1. С точки зрения надежности, это достаточно низкий показатель. Повышение надежности в таких сетях достигается введением резервных связей (например, защиты типа 1+1). Древовидная топология находит применение в локальных сетях, сетях абонентского доступа.

Топология «кольцо» (рис. 4) характеризует сеть, в которой к каждому пункту присоединены две, и только две линии. Кольцевая топология широко используется в локальных сетях, в сегментах меж-узловых соединений территориальных сетей, а также в сетях абонентского доступа, организуемых на базе оптического кабеля.

Число ребер графа, отображающего физическую топологию, равно числу вершин: R = n и характеризует сравнительно невысокие затраты на сеть.

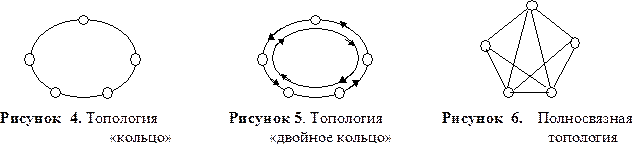
На логическом уровне между каждой парой пунктов могут быть организованы h = 2 независимых связывающих пути (прямой и альтернативный). Это обеспечивает повышение надежности связи в таком сегменте, особенно при использовании резервирования типа 1+1, так называемого двойного кольца (рис. 5). Двойное кольцо образуется физическими соединениями между парами пунктов, при которых информационный поток направляется в двух противоположных направлениях (восточном и западном), причем одно направление используется как основное, второе – как резервное.

Полносвязная топология (рис. 6) обеспечивает физическое и логическое соединение пунктов по принципу «каждый с каждым». Граф, включающий n вершин, содержит R = n (n – 1)/2 ребер, что определяет высокую стоимость сети. Количество независимых связывающих путей между каждой парой пунктов в таком сегменте сети равно h = n – 1. Полносвязная топология на логическом уровне обладает максимальной надежностью связи, благодаря возможности организации большого числа обходных путей. Такая топология характерна для территориальных сетей при формировании сегментов базовых и опорных (магистральных) сетей. Максимальная надежность связи в сегменте достигается при использовании на обходных направлениях альтернативных сред распространения сигналов (например, волоконно-оптический кабель и радиорелейная линия).

Ячеистая топология (рис. 7). Каждый пункт сегмента имеет непосредственную связь с небольшим числом пунктов, ближайших по расстоянию. При большом числе вершин число ребер R» rЧn /2, где r – число ребер, инцидентных каждой вершине. Ячеистые сегменты обладают высокой надежностью связи при меньшем числе ребер по сравнению с полно-связным сегментом.

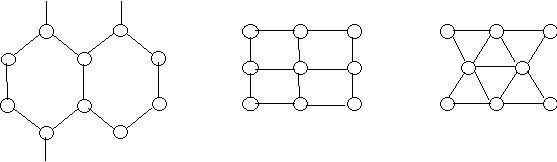
Рисунок. 7 Ячеистая топология

Использование полно-связной и ячеистой топологий целесообразно лишь в сегментах с высокой концентрацией трафика, так как их реализация связана со значительными затратами.

Сложные топологии. Реальные сети часто имеют сложные топологии, являющиеся расширениями и/или комбинациями базовых физических топологий. За счет использования сложных топологий удается обеспечивать требования к расширяемости и масштабируемости сети.

Под расширяемостью понимают возможность увеличения размера сети, путем сравнительно несложного включения новых структурных элементов. Расширяемость сети, как правило, ограничена, т.к. начиная с некоторого момента добавление очередного структурного элемента приводит к резкому снижению производительности сети.

Хорошо масштабируемые сети характеризуются неограниченными возможностями по наращиванию сети, не оказывающими влияния на ее производительность. Хорошая масштабируемость является одним из важнейших требований, предъявляемых к современным сетям, особенно территориальным.

Дата добавления: 2014-01-15