
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поняття функції та відображення
|
|
|
|
Поняття функції або відображення також є одним з центральних в математиці. В математичному аналізі прийнято наступне означення функції. Нехай задано множини 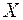 і
і 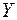 . Змінна
. Змінна 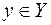 називається функцією від змінної
називається функцією від змінної  , якщо за деяким правилом кожному значенню
, якщо за деяким правилом кожному значенню  відповідає одне значення
відповідає одне значення 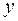 .
.
Розглянемо інше означення функції, яке є окремим випадком відношення між множинами. Функціональне відношення або функцію за традицією будемо позначати  .
.
Означення. Функцією називається бінарне відношення  між множиною
між множиною 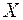 і множиною
і множиною 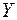 таке, що для кожного елемента
таке, що для кожного елемента  існує один і тільки один елемент
існує один і тільки один елемент 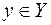 , відповідний елементу
, відповідний елементу  . Цей елемент називається значенням функції для елемента
. Цей елемент називається значенням функції для елемента  і позначається
і позначається 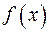 .
.
Інакше кажучи, функцією називається бінарне відношення, яке не містить двох пар з однаковими першими компонентами і різними другими.
Приклад. 1) 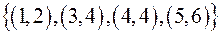 – функція;
– функція;
2)  – функція;
– функція;
 , де
, де 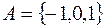 – функція;
– функція; 4) 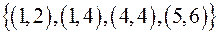 – відношення, але не функція.
– відношення, але не функція.
Функціональне відношення  зручно позначати ще так:
зручно позначати ще так:  або
або  (операторна форма запису).
(операторна форма запису).
Як і для звичайного відношення, для функціонального відношення множина 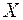 називається множиною відправлення, множина
називається множиною відправлення, множина 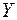 – множиною прибуття. Множина пар
– множиною прибуття. Множина пар 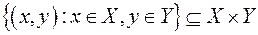 називається графіком функції
називається графіком функції  .
.
Множина 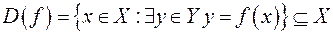 називається областю визначення функції
називається областю визначення функції  ; множина
; множина  називається областю значень функції
називається областю значень функції  .
.
Приклад. Для попереднього прикладу:
1)  ,
,  ;
;
2) 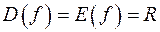 ;
;
3)  .
.
Відзначимо, що для будь-якої функції 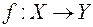 справедливе
справедливе  .
.
 використовується при означенні функції у двох розуміннях:1)
використовується при означенні функції у двох розуміннях:1)  – множина, елементами якої є пари
– множина, елементами якої є пари  , між якими існує функціональне відношення;2)
, між якими існує функціональне відношення;2) 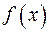 – позначення для елемента
– позначення для елемента 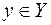 , що відповідає даному елементу
, що відповідає даному елементу  .
. Означення. Функції  і
і 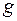 називаються рівними, якщо їхні області визначення збігаються і для кожного
називаються рівними, якщо їхні області визначення збігаються і для кожного 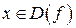
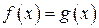 .
.
Для функцій широко застосовується геометрична термінологія. Функцію 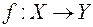 називають відображенняммножини
називають відображенняммножини 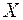 в множину
в множину 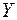 , елемент
, елемент 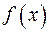 називається образом
називається образом  при відображенні
при відображенні  . Якщо
. Якщо 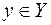 , то будь-який
, то будь-який  , для якого
, для якого  , називається прообразом елемента
, називається прообразом елемента  . Сукупність всіх прообразів елемента
. Сукупність всіх прообразів елемента 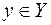 називається повним прообразом елемента
називається повним прообразом елемента  і позначається
і позначається  :
: 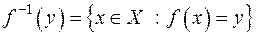 . Ясно, що
. Ясно, що  є підмножиною (можливо, порожньою) множини
є підмножиною (можливо, порожньою) множини 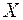 .
.
Аналогічно визначаються образ  множини
множини 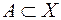 і прообраз
і прообраз  множини
множини  :
:
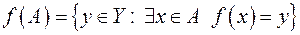 ;
;
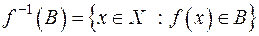
Зокрема,
 .
.
|

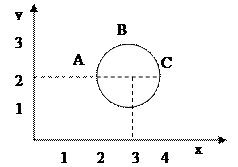
 Приклад. Коло радіуса 1 з центром у точці (3;2), тобто множина
Приклад. Коло радіуса 1 з центром у точці (3;2), тобто множина 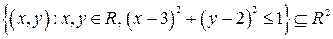 задає відношення між
задає відношення між  і
і  (віссю
(віссю  і віссю
і віссю  ). Образом числа 4 є число 2. Образом відрізка
). Образом числа 4 є число 2. Образом відрізка 
 є відрізок
є відрізок 
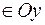 . Відрізок
. Відрізок  є прообразом числа 2. Це відношення не є функціональним. Прикладом функціонального відношення між дійсними числами на цьому ж малюнку може служити дуга
є прообразом числа 2. Це відношення не є функціональним. Прикладом функціонального відношення між дійсними числами на цьому ж малюнку може служити дуга  .
.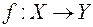 збігається з множиною
збігається з множиною 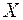 , тобто
, тобто  , то функція
, то функція 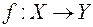 називається повною функцією, всюди або цілком визначеною функцією. При цьому кожному елементу множини
називається повною функцією, всюди або цілком визначеною функцією. При цьому кожному елементу множини  відповідає не більш ніж один однозначно визначений елемент множини
відповідає не більш ніж один однозначно визначений елемент множини 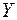 . Функція, яка не є повною, називається частковою (або не всюди визначеною, не цілком визначеною функцією).
. Функція, яка не є повною, називається частковою (або не всюди визначеною, не цілком визначеною функцією). Приклад:
Функція 
 – всюди визначена.
– всюди визначена.

 – не всюди визначена.
– не всюди визначена.
Означення. Відображення 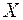 на
на 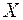 називається перетворенням множини
називається перетворенням множини 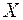 .
.
 відображає
відображає  в
в  ", навіть коли
", навіть коли  не є відображенням. Оскільки функції є бінарними відношеннями, то можна знаходити обернені функції і застосовувати операцію композиції.
не є відображенням. Оскільки функції є бінарними відношеннями, то можна знаходити обернені функції і застосовувати операцію композиції. Означення. Якщо відношення, обернене до функції 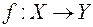 , є функціональним, то воно називається функцією, оберненою до
, є функціональним, то воно називається функцією, оберненою до  і позначається
і позначається  .
.
Оскільки в оберненому відношенні образи і прообрази міняються місцями, то обернена функція може не існувати.
Приклади:
1. Функція  відображає відрізок
відображає відрізок  на відрізок
на відрізок  . На відрізку
. На відрізку  для неї існує обернена функція
для неї існує обернена функція  .
.
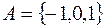 функція
функція  не має оберненої, оскільки
не має оберненої, оскільки 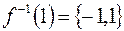 .
. Означення. Нехай задані функції 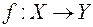 і
і 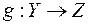 . Функція
. Функція 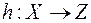 називається композицією функцій
називається композицією функцій  і
і 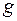 , якщо має місце рівність
, якщо має місце рівність 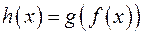 . Часто кажуть, що функція
. Часто кажуть, що функція 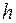 отримана підстановкою
отримана підстановкою  в
в 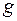 .
.
В математичному аналізі означення композиції двох функціональних відношень 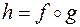 відповідає означенню складеної функції
відповідає означенню складеної функції 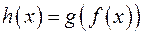 ..
..
В математичному аналізі розглядалися елементарні функції – композиції скінченного числа арифметичних функцій і основних елементарних функцій: степеневих, показникових, логарифмічних, тригонометричних.
Наприклад, функція  є елементарною, тому що вона є композицією функцій
є елементарною, тому що вона є композицією функцій  ,
,  ,
, 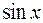 ,
, 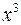 ,
, 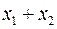 ,
,  ,
, 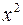
Означення. Вираз, що описує композицію функцій і містить функціональні знаки і символи аргументів, називається формулою.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1227; Нарушение авторских прав?; Мы поможем в написании вашей работы!