Метод со структурным резервированием элементов

Надежность выбранного квазиэлемента нужно повысить за счет резервирования без изменения надежности составляющих элементов. Для решения задачи, нужно последовательно увеличивать число резервных элементов, каждый раз определяя величину вероятности безотказной работы квазиэлементов при ч, до тех пор, пока не будет обеспечено необходимое значение .

Так как в нашем случае необходимо резервировать элементы двух квазиэлементов (F и C), то перед каждым добавлением нового резервного элемента нужно определять квазиэлемент в который его добавлять. То есть нужно добавлять новый резервный элемент в тот квазиэлемент (F или C), у которого меньше значение вероятности безотказной работы при ч.

В начальной схеме (рис. 1.2) наименьшее значение вероятности безотказной работы имеет квазиэлемент C (система «2 из 4»). Для повышения надежности системы «2 из 4» добавляем к ней элемент 16, идентичный по надежности исходным элементам 10 – 13 (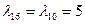), получаем систему «2 из 5»:

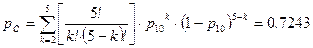.	(3.1)
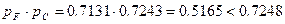.	(3.2)

Следующий резервный элемент нужно добавлять в квазиэлемент F, т.к. теперь он имеет наименьшее значение вероятности безотказной работы (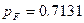) из F и C. Однако расчет показывает, что даже если удастся повысить значение вероятности безотказной работы квазиэлемента F до 100% (что на практике невозможно), значение общей вероятности безотказной работы будет меньше необходимого.

.

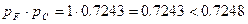(3.3)

Это значит, что новый резервный элемент (17) нужно добавлять снова в квазиэлемент C.

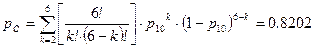.	(3.4)
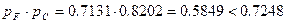.	(3.5)

Следующий резервный элемент нужно добавлять в квазиэлемент F, т.к. теперь он имеет наименьшее значение вероятности безотказной работы (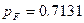) из F и C; и увеличение значения вероятности его безотказной работы может дать требуемую общую вероятность безотказной работы квазиэлементов F и C.

.

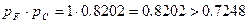(3.6)

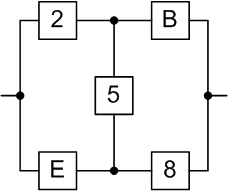
Рисунок 3.1 – Мостиковая схема квазиэлемента F

Для повышения надежности мостиковой схемы (рис. 3.1), выберем элемент с меньшим значением вероятности безотказной работы: 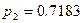, , 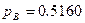, , 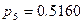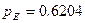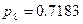. Элементы 5 или B имеют наименьшее значение вероятности безотказной работы 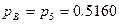. Так как для повышения вероятности безотказной работы всей мостиковой схемы повышение вероятности безотказной работы диагонального элемента (5) малоэффективно, выберем элемент B.

Квазиэлемент B состоит из последовательного соединения элементов 3 и 4. Для повышения вероятности безотказной работы квазиэлемента B, выберем любой из элементов (3 или 4), т.к. вероятность их безотказной работы одинакова (выбрали элемент 3). Добавляем новый резервный элемент (18) идентичный элементу 3:

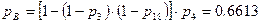.	(3.7)
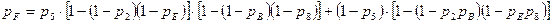
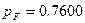.	(3.8)
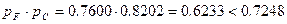.	(3.9)

Добавляем новый резервный элемент (19) идентичный элементу 4:

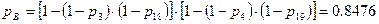.	(3.10)
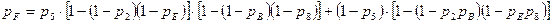
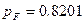.	(3.11)
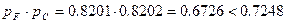.	(3.12)

Т.к. 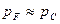, следующий резервный элемент (20) добавим в квазиэлемент C:

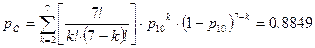.	(3.13)
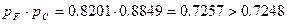.	(3.14)

Таким образом, для повышения надежности до требуемого уровня необходимо в исходной схеме (рис. 1.1) добавить элементы 16 – 20, как это показано на рис. 3.2.

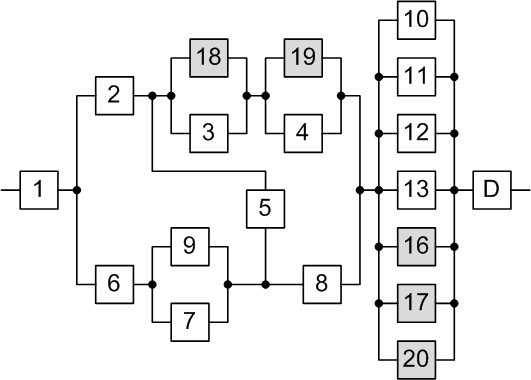
Рисунок 3.2 – Структурная схема системы после структурного резервирования

Результаты расчетов вероятностей безотказной работы квазиэлементов B``, C``, F`` и системы в целом P`` представлены в таблице 3.1.

Расчеты показывают, что при ч, 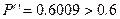, что соответствует условию задания.

На рис. 3.3 нанесны кривые зависимостей вероятности безотказной работы системы после повышения надежности элементов 2 – 13 (кривая Ph) и после структурного резервирования (кривая Pd).

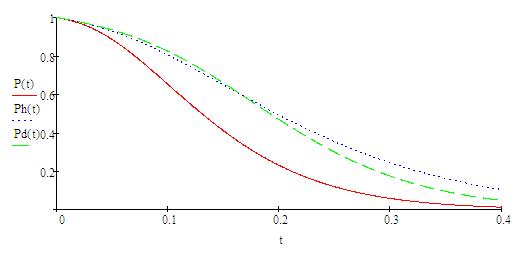
Рисунок 3.3 – Изменение вероятности безотказной работы исходной схемы P(t), системы с повышенной надежностью Ph(t) и системы со структурным резервированием элементов Pd(t)

Таблица 3.1 – Расчет вероятности безотказной работы системы

Элемент	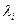, ×10^-6 ч^-1	Наработка t×10^6ч
0.05	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.1654
1,14,15		0.9512	0.9048	0.8607	0.8187	0.7788	0.7408	0.7047	0.6703	0.8475
2-4,6-8		0.9048	0.8187	0.7408	0.6703	0.6065	0.5488	0.4966	0.4493	0.7183
5,9		0.8187	0.6703	0.5488	0.4493	0.3679	0.3012	0.2466	0.2019	0.5160
10-13		0.7788	0.6065	0.4724	0.3679	0.2865	0.2231	0.1738	0.1353	0.4373
A	-	0.9827	0.9402	0.8831	0.8185	0.7513	0.6847	0.6207	0.5605	0.8636
B	-	0.8187	0.6703	0.5488	0.4493	0.3679	0.3012	0.2466	0.2019	0.5160
C	-	0.9639	0.8282	0.6449	0.4687	0.3246	0.2173	0.1419	0.0911	0.5881
D	-	0.9976	0.9909	0.9806	0.9671	0.9511	0.9328	0.9128	0.8913	0.9768
E	-	0.8892	0.7698	0.6542	0.5486	0.4557	0.3758	0.3082	0.2519	0.6204
F	-	0.9682	0.8786	0.7544	0.6204	0.4940	0.3840	0.2932	0.2211	0.7131
P	-	0.8856	0.6525	0.4106	0.2302	0.1188	0.0577	0.0268	0.0120	0.3471
2`-4`, 6`-8`	1.2162	0.9410	0.8855	0.8332	0.7841	0.7378	0.6943	0.6533	0.6148	0.8178
5`,9`	2.4325	0.8855	0.7841	0.6943	0.6148	0.5444	0.4820	0.4268	0.3779	0.6688
10`-13`	3.0406	0.8590	0.7378	0.6338	0.5444	0.4676	0.4016	0.3450	0.2963	0.6048
A`	-	0.9932	0.9753	0.9490	0.9168	0.8805	0.8416	0.8013	0.7604	0.9396
B`	-	0.8855	0.7841	0.6943	0.6148	0.5444	0.4820	0.4268	0.3779	0.6688
C`	-	0.9900	0.9421	0.8575	0.7509	0.6374	0.5276	0.4281	0.3418	0.8262
E`	-	0.9346	0.8636	0.7908	0.7189	0.6497	0.5843	0.5235	0.4675	0.7684
F`	-	0.9883	0.9531	0.8977	0.8276	0.7490	0.6673	0.5867	0.5102	0.8773
P`	-	0.9285	0.8051	0.6496	0.4921	0.3536	0.2433	0.1616	0.1042	0.6001
16``-18``		0.7788	0.6065	0.4724	0.3679	0.2865	0.2231	0.1738	0.1353	0.4373
19``,20``		0.9048	0.8187	0.7408	0.6703	0.6065	0.5488	0.4966	0.4493	0.7183
B``	-	0.9820	0.9354	0.8702	0.7944	0.7143	0.6343	0.5574	0.4855	0.8476
C``	-	0.9993	0.9828	0.9173	0.7954	0.6413	0.4859	0.3502	0.2427	0.8850
F``	-	0.986	0.9360	0.8514	0.7445	0.6295	0.5179	0.4168	0.3298	0.8201
P``	-	0.9351	0.8248	0.6591	0.4689	0.2990	0.1739	0.0939	0.0478	0.6009

Вывод:

1. Для повышения надежности и увеличения 60% - наработки системы в 1.5 раза (до ч) предложены два способа:

а) повышение надежности элементов 2 - 13 и уменьшение интенсивности их отказов в 1.6444 раз;

б) нагруженное резервирование элементов 3, 4, 10, 11, 12, и 13 соответственно идентичными по надежности резервными элементами 18, 19, 16, 17 и 20. (рис. 3.2).

2. Анализ зависимостей вероятности безотказной работы системы от времени (наработки) (рис. 3.3) показывает, что второй способ повышения надежности системы (структурное резервирование) предпочтительнее первого, так как в период наработки до ч вероятность безотказной работы системы при структурном резервировании (кривая Рd) выше, чем при увеличении надежности элементов (кривая Ph).

Дата добавления: 2014-01-15