Лекція 2. Однорідні ланцюги Маркова та їх використання в моделюванні економічних систем

1. Марківські випадкові процеси та однорідні ланцюги Маркова.

2. Матриця однокрокового переходу.

3. Ймовірності багатокрокових переходів системи. Вектор початкового стану.

4. Поглинальні ланцюги Маркова.

5. Потокові моделі з використанням поглинальних ланцюгів Маркова.

6. Регулярні ланцюги Маркова та числові характеристики для станів регулярних ланцюгів Маркова.

7. Ймовірності моделі з використанням регулярних ланцюгів Маркова.

1. Випадковий процес називається марківським, якщо для будь-якого моменту часу u при фіксованому значенні 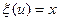(яким би не був х) випадкові величини 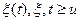не залежать від .

У випадку дискретних станів вводиться поняття ланцюга Маркова, а саме:

нехай досліджується певна система S, яка в кожний момент часу може перебувати в одному з несумісних станів і може змінювати ці стани у моменти часу Говорять, що послідовність станів утворює ланцюг Маркова, якщо умовна ймовірність переходу стану системи в момент часу t: 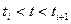в будь-який можливий стан 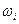залежить лише від того, в якому стані перебувала система в момент часу 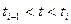і не залежить від того, в якому стані перебувала система в більш ранні моменти часу.

Матриця переходів:

,

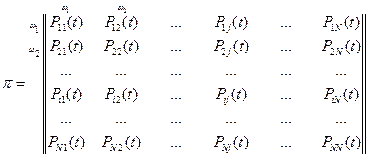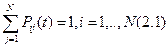
У випадку, коли не залежить від часу, говорять що ланцюг Маркова є однорідним.

2. Матриця однокрокового переходу для однорангового ланцюга Маркова має вигляд:

,

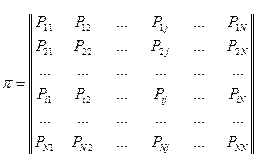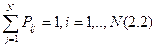
Ймовірність переходу системи зі стану 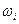в стан 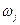за n кроків називається n – кроковою матрицею переходу. Нехай задана матриця однокрокового переходу . Знайдемо матрицю двокрокового переходу зі стану 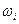в стан .

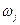3. Ймовірності багатокрокових переходів.

; .

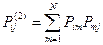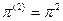Аналогічно: ; .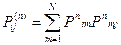

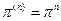Перший стан, в якому система знаходиться або визначається: (2.3).

Приклад 2.1

Відомо, що житель столиці може добиратися на роботу тролейбусом, автобусом, метро. Відомо, що коли він користується автобусом, то ймовірність, що наступного дня він поїде також автобусом 0,6, тролейбусом 0,35, метро 0,05. Якщо користується тролейбусом, то ймовірність повтору 0,7, зміни на автобус 0,25, метро 0,05. Якщо метро: ймовірність повтору 0,8, зміни на автобус 0,05, на тролейбус 0,15. Побудувати матрицю однокрокового переходу.

Якщо у понеділок їхав у метро, знайти ймовірність того, що у середу буде користуватися автобусом, у п’ятницю автобусом.

1 – автобус; 2 – тролейбус; 3 – метро.

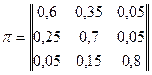
Середа: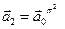

П’ятниця:

4. Ланцюг Маркова називається поглинальним, коли існує хоча б один стан, потрапляючи в який, процес у ньому залишається.

Основні питання:

– ймовірність переходу в поглинальний стан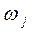за умови, що процес почався з не поглинального стану ;

– середнє значення часу перебування процесу у не поглинальних станах до моменту його переходу у поглинальний стан за умови, що в початковий момент він перебував у певному не поглинальному стані ;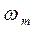

– середня кількість кроків до переходу процесу в деякий поглинальний стан за умови, що в початковий момент він перебував у не поглинальному стані .

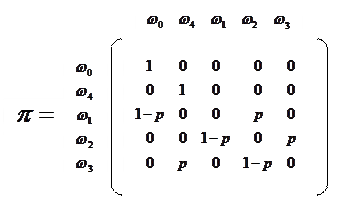
Структуризуємо матрицю 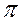: поглинальні стани позначимо першими номерами 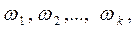решта станів не поглинальні.

Матриця 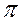приводиться до канонічного вигляду поділившись на чотири блоки:

I – одинична матриця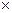 kk;

O – нульова матриця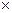 kN-k;

R –матриця N-k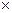k, що визначає ймовірності переходу з не поглинальних станів у поглинальні;

Q – матриця N-k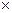N-k, що визначає перехід з не поглинальних станів у не поглинальні.

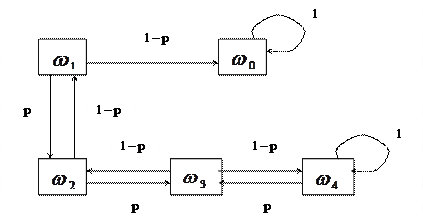
Приклад 2.2

Гравець має m євро і захотів виграти 4m євро. Ймовірність, що він виграє одну гру – р. побудувати імовірнісний граф і матрицю 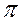для цього прикладу.

Позначимо: 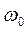– стан, коли гравець програв, 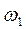– початковий стан, 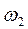– має 2m євро, 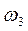– має 3m євро, – має 4m євро.

;

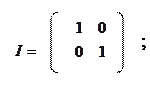
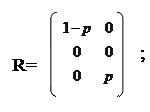
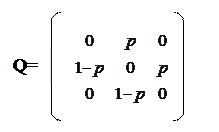
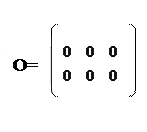
Для поглинальних ланцюгів важливе значення має матриця Q. Її властивості:

1. ;

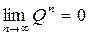2. Матриця I – Q має обернену 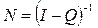яка називається фундаментальною для поглинальних ланцюгів Маркова.

Елементи фундаментальної матриці являють собою математичне сподівання перебування процесу у відповідних станах 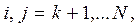а – середня кількість кроків процесу до моменту, коли він потрапить у поглинальний стан, за умови, що початковий його стан .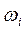

Нехай функція, що дорівнює загальній кількості моментів часу, протягом якого процес перебуває у не поглинальному стані .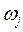

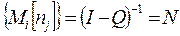(2.5)

Числова характеристика 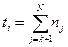означає математичне сподівання часу перебування процесу у відповідному не поглинальному стані .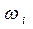

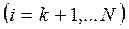Приклад 2.3

У прикладі 2.2 нехай р=0,6.

Q=

; ; .

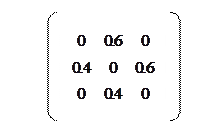
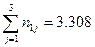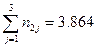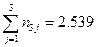По визначенню дисперсії:

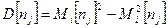
Використавши матричну форму запису послідовно отримаємо:

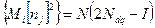(2.6)

де 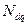– матриця, отримана з фундаментальної з збереженням лише діагональних елементів, решта – нулі.

(2.7)

де .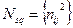

Приклад 2.4

знайти дисперсію для матриці N, знайденої у прикладі 2.3.

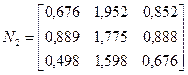
Ввівши вектор , у матричному вигляді:

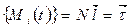(2.8)

При визначенні дисперсії, послідовно знаходимо:

;

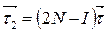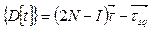(2.9)

де .

Таким чином, дисперсія числа кроків визначається вектором:

.

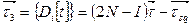Приклад 2.5

Знайти вектор дисперсії часу, використовуючи дані прикладів 2.3 та 2.4. Дати імовірнісне тлумачення отриманим результатам.

Якщо початковий стан процесу задається вектором:

,

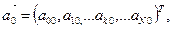
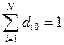де 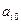імовірнісні перебування процесу у відповідному стані у початковий момент часу, то вектор

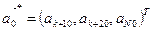
задає ймовірності, що визначають в момент не поглинальні стани.

Числові характеристики переходу системи у не поглинальні стани у матричному вигляді такі:

(2.10)

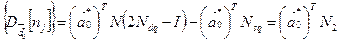(2.11)

(2.12)

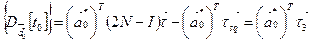(2.13)

Приклад 2.6.

Для вектора початкового розподілу

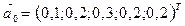
обчислити числові характеристики переходу.

Нехай – ймовірність того, що процес перебуваючи у не поглинальному стані 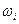потрапить у поглинальний стан :

, , .

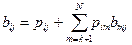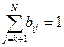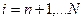Якщо ввести матрицю , то в матричному вигляді ,звідки

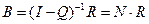(2.14)

Приклад 2.7.

Використавши умову прикладів 2.2 та 2.3 визначити матрицю В та дати її елементам економічне тлумачення.

; .

5. В термінах ймовірності та марковських процесів можна сформулювати багато економічних задач.

Дата добавления: 2014-01-11