Структура механизмов

Среди всего многообразия конструкций механизмов различают: стержневые (рычажные), кулачковые, фрикционные, зубчатые механизмы, механизмы с гибкими звеньями (например, ременные передачи) и др. виды.

Менее распространенные классификации подразумевают наличие механизмов с низшими или высшими парами в плоском или пространственном исполнении и т.д.

Учитывая возможность условного превращения практически любого механизма с высшими парами в рычажный, в дальнейшем наиболее подробно рассматривается именно эти механизмы, а структурные схемы других механизмов изложены в соответствующих разделах.

Среди рычажных механизмов наиболее распространены так называемые четырехзвенные, примеры которых представлены на рисунке.

Виды звеньев (см. рисунок):

стойка – звено, принимаемое за неподвижное; такое звено в механизме может быть только одно;

кривошип – вращающееся звено рычажного механизма, которое может совершать полный оборот вокруг неподвижной оси;

коромысло – вращающееся звено рычажного механизма, которое может совершать только неполный оборот вокруг неподвижной оси;

шатун – звено рычажного механизма, образующее кинематические пары только с подвижными звеньями;

кулиса – звено рычажного механизма, вращающееся вокруг неподвижной оси и образующее с другим подвижным звеном поступательную пару; в зависимости от степени протяженности элемента поступательной пары различают «камень» (звено меньшей протяженности) и «направляющую»;

ползун – звено рычажного механизма, образующее поступательную пару со стойкой;

кулачок – звено, имеющее элемент высшей пары, выполненный в виде поверхности переменной кривизны;

камень – звено, совершающее поступательное движение относительно подвижной направляющей, называемой кулисой;

зубчатое колесо – звено с замкнутой системой зубьев, обеспечивающее непрерывное движение другого зубчатого колеса или рейки.

Количество типов и видов механизмов исчисляется тысячами, поэтому классификация их необходима для выбора того или иного механизма из большого ряда существующих, а также для проведения синтеза механизма.

Универсальной классификации нет, но наиболее распространены 3 вида классификации:

Функциональная. По принципу выполнения технологического процесса механизмы делятся на механизмы: приведения в движение режущего инструмента; питания, загрузки, съёма детали; транспортирования и т.д.;

Структурно-конструктивная. Предусматривает разделение механизмов как по конструктивным особенностям, так и по структурным принципам. К этому виду относят механизмы: кривошипно-ползунный; кулисный; рычажно-зубчатый; кулачково-рычажный и т.д.;

Структурная. Проста, рациональна, тесно связана с образованием механизма, его строением, методами кинематического и силового анализа, была предложена Л.В. Ассуром[2] в 1916 году и основана на принципе построения механизма путем наслоения (присоединения) кинематических цепей (в виде структурных групп) к начальному механизму. Согласно этой классификации, любой механизм можно получить из более простого присоединением к последнему кинематических цепей с числом степеней свободы W = 0, получивших название структурных групп, или групп Ассура. Недостаток классификации – неудобство для выбора механизма с требуемыми свойствами.

Структурная классификация механизмов по Ассуру Л.В.

Для решения задач синтеза и анализа сложных рычажных механизмов профессором Петербургского университета Ассуром Л.В. была предложена оригинальная структурная классификация. По этой классификации механизмы не имеющие избыточных связей и местных подвижностей состоят из первичных механизмов и структурных групп Ассура (см. рисунок).

Под первичным механизмом понимают механизм, состоящий из двух звеньев (одно из которых неподвижное) образующих кинематическую пару с одной W_пм=1 или несколькими W_пм > 1 подвижностями. Примеры первичных механизмов даны на рисунке.

Структурной группой Ассура (или группой нулевой подвижности) называется кинематическая цепь, образованная только подвижными звеньями механизма, подвижность которой (на плоскости и в пространстве) равна нулю (W_гр = 0).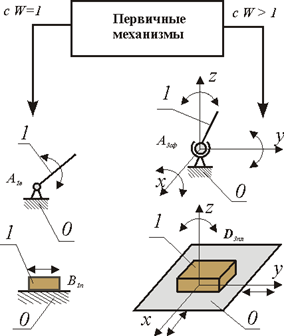

Конечные звенья групп Ассура, входящие в две кинематические пары, из которых одна имеет свободный элемент звена, называются поводками.

Группы могут быть различной степени сложности. Структурные группы Ассура делятся на классы в зависимости от числа звеньев, образующих группу, числа поводков в группе, числа замкнутых контуров внутри группы. В пределах класса (по Ассуру) группы подразделяются по числу поводков на порядки (порядок группы равен числу ее поводков). Механизмы классифицируются по степени сложности групп входящих в их состав. Класс и порядок механизма определяется классом и порядком наиболее сложной из входящих в него групп. Класс группы задается наивысшим замкнутым контуром, входящим в ее состав. Класс же контура определяется числом внутренних кинематических пар, образующих этот замкнутый контур. Можно сказать, что:

а) в группу Ассура II-го класса входит прямолинейный контур (табл.);

б) в группу Ассура III-го класса – трехсторонний контур ABC (рисунок (б));

в) в группу Ассура IV-го класса – четырехсторонний подвижный контур BCDE (рисунок).

На следующем рисунке также приведены примеры групп Ассура.

Рассмотрим подробнее принцип нахождения класса группы.

Класс групп, состоящих более чем из двух звеньев, определяется числом вершин (или сторон) многоугольника, образуемого внутренними кинематическими парами на структурной схеме группы, которая строится по следующим правилам:

- все вращательные и поступательные пары пятого класса изображают на этой схеме как вращательные;

- звенья, участвующие в нескольких кинематических парах, изображаются в виде соответствующих многоугольников.

На рисунках для удобства сопоставления помещены рядом друг с другом кинематические и структурные схемы двух групп различных классов.

На структурной схеме для большей наглядности можно те шарниры, которым на кинематической схеме соответствуют поступательные пары, помечать буквой «п».

В структурных схемах групп III класса внутренние шарниры образуют один или несколько треугольников жесткой (неизменяемой) конфигурации; в схемах групп более высоких классов встречаются многоугольники (изменяемой конфигурации) с четырьмя и большим числом сторон, которое и определяет класс группы.

Отметим, что классификации Л. В. Ассура подчиняются только те плоские механизмы, у которых начальные звенья образуют кинематические пары со стойкой.

Наиболее распространённые структурные группы 2-го класса подразделяются на 5 видов (модификаций) (см. табл.).

Особенность структурных групп Ассура - их статическая определимость. Если группу Ассура свободными элементами звеньев присоединить к стойке, то образуется статически определимая ферма. Используя группы Ассура, удобно проводить структурный, кинематический и силовой анализ механизмов.

Для определения класса механизма его расчленяют на структурные группы, начиная с конца механизма. За начало механизма принимают ведущее звено (начальный механизм).

От конца механизма отделяются поочерёдно простейшие структурные группы до тех пор, пока не останется лишь механизм 1-го класса (начальный механизм, их может быть несколько).

По классу структурных групп определяют класс механизма. Количество начальных механизмов равно величине W.

Пример расчленения плоского рычажного механизма на структурные группы показан на рисунке. Предварительно вычисляют степень подвижности механизма W по формуле

В данном случае W = 1, а это значит, что в механизме должны быть одно ведущее звено и соответственно один начальный механизм.

Дата добавления: 2014-01-20