Замена высших кинематических пар низшими

Как известно, плоские звенья могут иметь звенья, входящие как в низшие, так и в низшие пары. При изучении структуры и кинематики плоских механизмов во многих случаях удобно заменять высшие пары кинематическими цепями или звеньями, входящими только в низшие вращательные и поступательные пары 5–го класса.

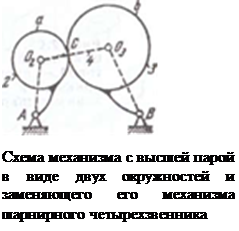При этой замене должно удовлетво­ряться условие, чтобы механизм, полученный после такой за­мены, обладал прежней степенью свободы и чтобы сохранились относительные в рассматриваемом положении движения всех его звеньев. Рассмотрим трехзвенный механизм, показанный на рисунке.

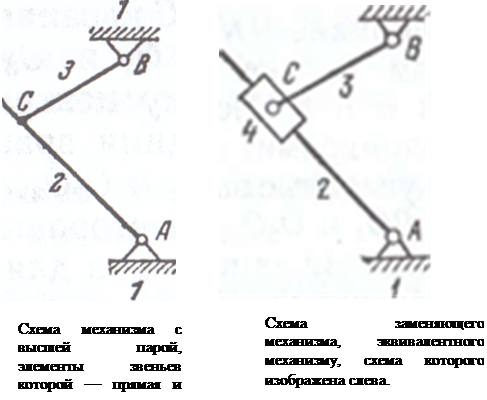
Механизм состоит из двух подвижных звеньев2 и3, входящих во вращательные пары V класса А и В со стойкой 1 и высшую пару С IV класса, элементы звеньев а и b которой представляют собою окружности радиусов 0₂С и 0₃С. Согласно формуле Чебышева степень свободы механизма будет

Можно показать, что рассматриваемый механизм может быть заменен эквивалентным ему механизмом шарнирного четырехзвенника АО₂О₃В. Высшая пара IV класса в точке С заменяется звеном 4, входящим в точках 02 и 03 во вращательные пары V класса. Полученный в результате замены механизм АО₂О₃В называется заменяющим механизмом.

Степень свободы W заменяющего механизма будет той же, что и у заданного механизма:

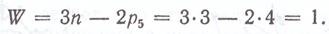
Так как элементы а и b звеньев являются окружностями с центрами в точках О₂ и О₃, то длина О₂О₃ звена 4 оказывается постоянной. Точно так же будут постоянными и длины АО₂ и ВО₂ звеньев 2 и 3. Заменяющий механизм АО₂О₃В эквивалентен заданному и с точки зрения законов движения звеньев 2 и 3.

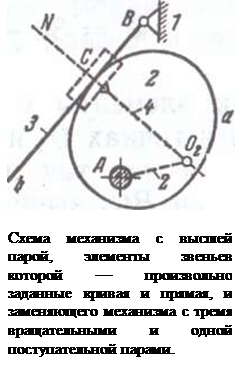
Рассмотренный способ получения заме­няющего механизма можно обобщить. Пусть задан механизм с высшей парой, элементы звеньев которой представляют собой произ­вольно заданные кривые а и b (рисунок). Для построения схемы заменяющего механизма про­водим нормаль NN в точке С касания кривых и отмечаем на ней центры О₂и О₃ кривизны кривых а и b. По-прежнему центры кривизны О₂и О₃ мы счи­таем шарнирами, образующими вращательные пары, в которые входят условные звенья АО₂ и О₂О₃, с одной стороны, и условные звенья ВО₃ и О₂О₃, с другой стороны.

Описанная замена правильна для заданного положения основ­ного механизма. В другом положении схема заменяющего меха­низма останется той же, размеры же его звеньев изменятся, поскольку центры кривизны О₂ и О₃ сместятся.

Из дифференциальной геометрии известно, что окружность кривизны в точке касания с кривой и сама кривая эквивалентны до производных второго порядка включительно, и поэтому заме­няющий механизм эквивалентен основному в такой же степени, т. е. положения, скорости и ускорения одноименных точек того и другого механизма будут одинаковыми.

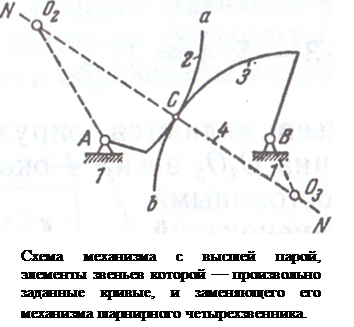
Если один из соприкасающихся элементов будет пред­ставлять собой некоторую кривую a, а второй прямую b (рисунок), то центр кривизны второго профиля будет бесконечно удален.

Условное звено 4 в этом случае будет входить в центре кривизны О₂ элемента 2 во вращательную пару V класса. Вторая вращательная пара, в которую должно входить звено 3, имеет бесконечно удаленную ось вращения и переходит в поступательную пару также V класса.

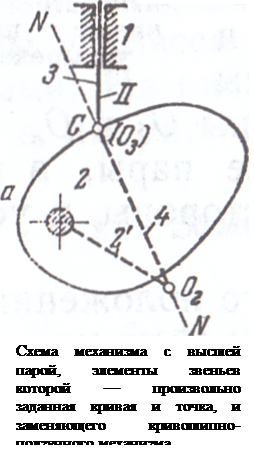
Далее возможен случай, когда один из соприкасающихся элементов — кривая а, а другой — точка С (рисунок). В этом случае центр кривизны О₃ элемента С совпадает с самой точкой С, и поэтому условное звено 4 должно входить в две вращательные пары V класса — во вращательную пару с осью, проходящей через центр кривизны О₂ криволинейного элемента а, и во вращательную пару с осью, проходящей через точку С.

В том случае, когда одним элементом является прямая АС, а другим — точка С (рисунок), замена сводится к постановке условного звена 4, входящего в одну поступательную и одну вращательную пары.

Ось вращательной пары и ось движения поступательной пары должны проходить через точку соприкосновения С.

Таким образом, любой плоский механизм с высшими парами IV класса может быть заменен механизмом, в состав которого входят только низшие кинематические пары V класса.

Если все высшие пары IV класса в плоском механизме заменены низшими парами, то структурная формула для заменяющего механизма получит вид

Дата добавления: 2014-01-20