Понятие о картографических проекциях

Изучение земной поверхности обычно ведётся по уменьшенным её изображениям. Поверхность Земли в целом наглядно и в подобном виде можно изобразить лишь на модели её, которая называется глобусом. Однако размеры глобусов не дают возможности для подробного изображения земной поверхности. Глобус, имеющий диа­метр в 1,3 м и являющийся сравнительно громоздким, представляет уменьшение размеров Земли в 10 000 000 раз. В силу этого подроб­ные изображения земной поверхности в целом и по частям делаются на плоскости, главным образом на бумаге.

Так как физическая поверхность Земли имеет совершенно непра­вильную кривую форму, то на плоскости изображают не действитель­ные очертания этой поверхности, а проекции их на уровенную по­верхность.

Проектирование точек физической поверхности Земли на уровен­ную поверхность производится с помощью отвесных линий. Как уже известно, вместо уровенной поверхности, которая не определяется

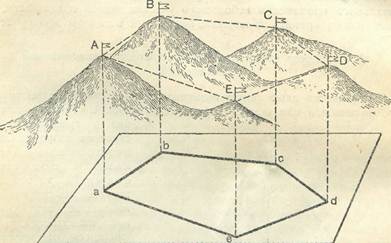
Рис. 5 Горизонтальное проложение участка земной поверхности.

математически, берётся поверхность эллипсоида или шара. Поверх­ность эллипсоида и шара не развёртывается на плоскости без скла­док и разрывов, в чём легко убедиться, распластав на плоскости бу­мажную шаровую оболочку. Эти складки и разрывы указывают на то, что плоские изображения поверхности земного эллипсоида или шара всегда будут сопровождаться искажениями. Размеры иска­жений получаются тем значительнее, чем больше изображаемая часть этой поверхности. Однако можно взять такую небольшую часть этой поверхности, при изображения которой на плоскости искажения будут меньше точности измерений и графических построений. Эти искаже­ния не могут нами ощущаться, а потому плоское изображение взя­той части земной поверхности можно с полным основанием считать неискажённым. В таком случае часть поверхности земного эллипсоида или шара заменяется горизонтальной плоскостью, которая касательна к ней в средней точке, и проектирование точек При создании карт поверхность эллипсоида вращения, как ма- тематическая поверхность Земли, не может быть развернута наплоскости без складок или разрывов, поэтому используют кар -| тографические проекции, в которых отображение поверхности эллипсоида на плоскости происходит по определенным матема­тическим законам. Эти законы выражают функциональную связь координат точек картографируемой поверхности и плоскости.

В основу такого отображения картографической проекции по­ложена система геодезических координат, координатными лини­ями которой являются меридианы и параллели. Линии меридиа­нов на картографируемой поверхности получают путем сечения ее плоскостями, проходящими через ось вращения эллипсоида (они будут эллипсами), а линии параллелей — путем сечения кар­тографируемой поверхности плоскостями, перпендикулярными к оси вращения эллипсоида (параллели имеют вид окружностей). Эти же координатные сетки в виде меридианов и параллелей на картах строят по определенным математическим правилам.

Возможен выбор различных правил перехода к плоскости, т.е. построение изображения в разных картографических проекциях. Математическая основа картографических проекций позволяет производить на картах точные измерения. Однако для этого нужно знать закон распределения искажений каждой проекции.

Картографические проекции различают по разнообразным при­знакам, прежде всего по характеру сохраняемых свойств и виду сетки меридианов и параллелей. По первому признаку проекции делят на:

равновеликие, сохраняющие площади;

равноугольные (или конформные) проекции, которые сохраняют углы и, следовательно, формы контуров, но сильно искажают соотношение размеров (например, проекция Меркатора);

проекции, сохраняющие длины линий в некоторых направлениях или во всех направлениях из одной какой-нибудь точки;

производные, не сохраняющие полностью никаких свойств, но более или менее удобные для потребителя карты, распределяю­щие искажения по всему изображению.

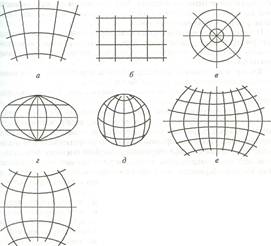
По виду сетки меридианов и параллелей проекции подразде­ляют на следующие основные виды, обозначенные на рис. 6.

В нормальной конической проекции меридианы изображают пря­мыми линиями, сходящимися в одной точке. Параллели — дуги концентрических окружностей, центр которых находится в точке схода меридианов. Радиусы параллелей зависят от условий равно-угольности или равновеликости.

В нормальной цилиндрической проекции меридианы и параллели изображают взаимно-перпендикулярными прямыми линиями.

Рис. 6 Проекции:

а - коническая; б - цилиндрическая; в

азиму­тальная; г — псевдоцилиндрическая; д - псевдо­коническая; е - поликоническая; ж - псевдо­азимутальная

По свойствам изображения они могут быть равноугольными, равно­великими и производными.

В азимутальной проекции меридианы изображают прямыми ли­ниями, пересекающимися в одной точке. Параллели — концент­рические окружности с центром в точке пересечения меридианов. Применяются для территорий округлой формы и карт мелких масштабов.

На псевдоцилиндрических проекциях параллели изображают пря­мыми линиями. Меридианы — кривые: синусоиды или эллипсы. Применяются при создании карт океанов или всей Земли мелко­го масштаба.

На псевдоконических проекциях параллели изображают дугами концентрических окружностей. Меридианы — кривые, симмет­ричные относительно осевого меридиана. Применялись ранее для карт отдельных государств; теперь используются для показа по­верхности всей Земли и других планет.

На поликонической проекции параллели изображают дугами эк­сцентрических окружностей, центры которых находятся на осе-

вом прямолинейном меридиане. Меридианы — кривые, симмет­ричные относительно осевого прямолинейного меридиана. При­меняется для создания карт мира.

На псевдоазимутальных проекциях параллели изображают кон­центрическими окружностями. Меридианы — кривые, за исключением двух взаимно-перпендикулярных, которые служат осями симметрии.

Круговые проекции имеют параллели и меридианы, изображае­мые окружностями или дугами окружностей.

Производные проекции получают различными видоизменения­ми имеющихся проекций.

В геодезии и топографии применяют проекцию Гаусса - Крюгера -это такое конформное (равноугольное) изображение поверх­ности земного эллипсоида на плоскости, при котором осевой меридиан изображают прямой линией с сохранением масштаба, экватор — также прямой, перпендикулярной осевому меридиану, а все остальные меридианы и параллели — кривые линии. Проек­цию Гаусса - Крюгера нередко истолковывают как поперечную цилиндрическую равноугольную проекцию (Меркатора), но это неточно.

Систему координат Гаусса - Крюгера не следует отождествлять с применяемой за рубежом зональной системой координат в по­перечно-цилиндрической проекции Меркатора. Их главное отличие состоит в том, что в про­екции ПТМ проектирование земного эллипсоида сначала произ­водится на сферу, а затем на плоскость в проекции Гаусса - Лам­берта с дальнейшим равноугольным преобразованием элементов проекции Гаусса - Ламберта на плоскости с условием сохранения постоянного масштаба по осевому меридиану. По двум меридиа­нам, удаленным от осевого меридиана примерно на 180 км в обе стороны, масштаб длин т = 1, а по существенно ослож­няется математическая обработка сетей.осевому меридиану масштаб составляет 0,999 60. Этим достигаются меньшие искажения на краях зоны, чем в проекции Гаусса участка физической плоскостью, которая касательна к ней в средней точке.

Дата добавления: 2014-01-20