Количество информации в системе событий с различными вероятностями. Подход Шеннона

На практике, как правило, экспериментатор располагает некоторыми сведениями о свойствах исследуемого объекта, что позволяет делать предсказания. Следовательно, в этом случае различные исходы опыта уже не равновероятны.

Рассмотрим следующий эксперимент. Человек открывает страницу книги и наугад выбирает одну букву. Какой результат он получит? Процесс естественного развития языков привел к тому, что различные буквы встречаются в текстах с неодинаковыми частотами. Вероятности появления, или относительная частота появления в тексте букв в русском языке приведены в таблице 1, относительная частота появления пробела или знака препинания в русском языке составляет 0,174.

Таблица 1. Относительная частота появления в тексте букв в русском языке

Б	Частота	Б	Частота	Б	Частота	Б	Частота
о	0.09		0.038	з	0.016	ж	0.007
е, ё	0.072	л	0.035	ы	0.016	ш	0.006
а	0.062	к	0.028	б	0.014	ю	0.006
и	0.062	м	0.026	ь,ъ	0.014	ц	0.004
н	0.053	д	0.025	г	0.013	щ	0.003
т	0.053	п	0.023	ч	0.012	э	0.003
с	0.045	у	0.021	й	0.01	ф	0.002
р	0.04	я	0.018	х	0.009

Из табл.1 видно, что из 1000 наудачу выбранных в тексте букв около 90 раз встретится буква "о", 62 раза - "а", 26 раз-"м" и только 2 раза - "ф".

Таким образом, имея приведенную в таблице информацию можно априори предсказать, что в результате опыта экспериментатор с вероятностью р_о = 0,090 выберет букву "о", а с вероятностью р_е = 0,072 - букву "е" и т.д.

Вопросы оценки количества информации, получаемой в опыте с неравновероятными результатами были рассмотрены Клодом Шенноном.

Предположим, что в эксперименте измеряются значения некоторой дискретной случайной величины X. Совокупность всех возможных значений величины X образует полную систему взаимонезависимых случайных событий, называемую ансамблем:

(9)

где x_i (i = 1,2,…., N)- значения случайной величины X, которые она может принять в результате проведения опыта; p_i (i = 1,2,…., N) - вероятности получения соответствующих значений x_i. Поскольку cиcтема событий полная, выполняется условие нормировки

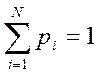(10)

Предположим далее, что в результате проведения одного опыта с полной определенностью стало известно, что случайная величина приняла некоторое значение x_k (1≥ k ≤ N). Количество информации, полученное в этом опыте, по определению считается равным

I_k = - log₂ p_k, (11)

где p_k - априорная вероятность события "Случайная величина приняла значение x_k ". Величина I_k называется частной информацией, поскольку она характеризует неожиданность появления отдельного конкретного события (Х = x_k). Из соотношения (11) видно, что наибольшая информация достигается, если в результате опыта произошло наименее вероятное событие. Заметим, что количество информации в виде (11) всегда положительно, постольку в соответствии с условием (10) вероятность каждого из событий всегда меньше единицы.

Усредненной оценкой количества информации при многократных повторениях опыта по измерению величины X является математическое ожидание частной информации – мера Шеннона:

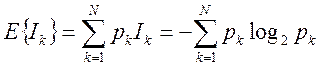. (12)

Мера Шеннона характеризует количество информации, приходящееся в среднем на одно событие.

Свойства меры Шеннона:

1) обращается в нуль, когда одно из состояний достоверно, а другие невозможны;

2) достигает максимального значения, когда состояния системы равновероятны, например: p₁ = p₂ = 0.5, E = -(0.5log(1/2) + 0.5log(1/2)) = 1, если p₁ = 0.25 p₂ = 0.75 то E = -(-0.75* 0.415 - 0.25*2) = 0.811;

3) является монотонно возрастающей функцией N;

4) обладает свойством аддитивности, то есть в случае объединения независимых систем их информации складываются.

На выходе реальных информационных систем количество информации, содержащееся в сообщении, определяется следующим образом:

I = Н_и - Н₀ , (13)

где I - количество информации, содержащееся в сообщении; Н_и - исходная неопределенность ансамбля событий, известная априори; Н₀ - неопределенность ансамбля событий, оставшаяся после опыта. До получения информации ситуация характеризуется неопределенностью того, от какого источника она будет направлена, т.е. априорной энтропией:

. (14)

Энтропия дискретной случайной величины — это минимум среднего количества бит, которое нужно передавать по каналу связи о текущем значении данной случайной величины.

В термодинамике энтропия означает вероятность теплового состояния вещества, в математике – степень неопределенности ситуации или задачи, в информатике она характеризует способность источника отдавать информацию. Энтропия источника бинарных (двоичных) сообщений изменяется от нуля до единицы в зависимости от вероятности сообщений и имеет максимум при p₁ = p₂ = 0,5. В этом случае мера Шеннона совпадает с мерой Хартли. Источник с энтропией в 1 бит полностью согласован с каналом, например, реле, имеющим информационную емкость в 1 бит. При неравновероятности сообщений канал будет недогружен. Зависимость энтропии от вероятности для бинарного источника иногда называют функцией Шеннона (рис. 41.)

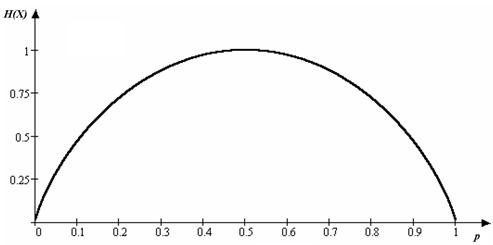
Рис. 41. Энтропия бинарного источника

Таким образом, маловероятное событие несет большее количество информации, чем событие высоковероятное. Это свойство количества информации соответствует психологической реакции человека. Действительно, как показано в экспериментальных исследованиях, чем неожиданнее происходящее перед глазами человека событие, тем больше соответствующее ему время задержки реакции человека на это событие. При этом соблюдается пропорциональная зависимость между временем задержки и количеством информации, найденным по формуле (11).

Для примера на рис. 42 за­имствованном из работы американского психолога Р. Xаймана кружками отмечены данные восьми опытов, состоящих в определении среднего времени, тре­бующегося испытуемому, чтобы указать, какая из k лам­почек (где k менялось от 1 до 8) зажглась.

Рис.42. Опыт с лампочками

Это среднее время определялось из большого числа серий зажиганий, в каждой из которых частоты зажиганий всех лампочек были одинаковыми, причем предварительно испытуемый специально тренировался в подобных опытах. По оси ординат на рис. 42 отложено среднее время реакции, а по оси абсцисс — величина log₂ k; при этом, как мы видим, все 8 кружков довольно точно укладываются на одну прямую.

§1.3. Обобщенная схема информационной системы

Использование информации связано с ее передачей от источни­ка к потребителю. В общем случае система передачи информации, состоит (рис.43) из источника сообщений (information source), передатчика (transmitter), линии связи (signal, received signal), приемника (receiver) и адресата (destination). Она оперирует сообщениями (message), сигналами, шумами (noise source).

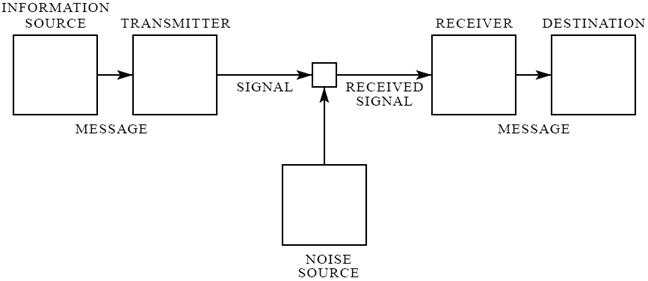
Рис.43. Обобщенная схема информационной системы из статьи К. Шеннона

Под сообщением понимают реализацию случайного процесса, представленного в форме последовательности дискретных символов (букв, цифр, знаков), последовательности значений физических величин (результатов измерения потока излучения или напря­жения на фотодиоде) через определенный интервал времени, непрерывных времен­ных или пространственных функций (развертка телевизионного кад­ра, фотоснимок, чертеж, изображение). Источник сообщений осуществляет выбор кон­кретного сообщения из ансамбля возможных сообщений. Источниками информации могут быть человек, фотоприемное устройство, различ­ные датчики физических величин, измерительные устройства и т.п. Передатчик перерабатывает сообщения в сигналы, со­ответствующие свойствам данного канала. Под сигналом понимается некоторая физическая величина, изменениями которой отображается сообщение. Обычно передатчик состоит из кодирующего устройства и модулятора.

В телефонной системе связи передатчиком слу­жит микрофон, осуществляющий преобразование звука в модулированный электрический ток, который затем передается по двухпро­водной линии связи. В телеграфном передатчике символы исходно­го сообщения (буквы, цифры, знаки) сначала кодируются (преобразуются в последовательности вторичных символов в виде точек и тире). Затем с помощью модулятора они преобразуются в конкрет­ный сигнал (электрический ток) передаваемый по линии связи. В лазерной системе связи сообщение (последовательность звуков) преобразуется в изменения амплитуды, фазы или частоты электромагнитного поля излучения. Сочетание источника сообщений с пе­редатчиком будем называть источником сигнала.

Линия связи - это тракт движения сигнала, физическая среда (коаксиальный кабель, оптоволокно, и т.д.), осуществляющая перенос информации от передатчика к приемнику. Устройство, включающее в себя передатчик, линию свя­зи и приемник, называют каналом связи.

В процессе передачи по линии связи сигнал может быть иска­жен помехами (шумами). С целью учета влияния шумов, создаваемых внешними и внутренними источниками или наложением других сигналов, в блок-схему введен эквивалентный источник по­мех. При этом на выходе линии связи вместо исходного неискаженного сигнала имеем сигнал с наложенным на него шумом. Искажение сообщений помехами исключают посредством помехоустойчивого кодирования и декодирования информации в передатчике и приемнике, соответствен­но.

Приемник восстанавливает сообщение из сигнала, выпол­няя преобразования, обратные преобразованиям передатчика.

Адресат - это лицо или аппарат, для которого предназ­начено сообщение. Как правило, адресат обладает свойствами запо­минания и обработки информации, а иногда и свойством управления.

Источники информации делятся на дискретные и непрерывные. Непрерывный источник выдает информацию в виде непрерывных функций времени, координат или того и другого вместе. Дискретный источник выдает информацию символ за символом в соответствии с вероятностями появления символов и их сочетаний.

К дискретным источникам информации относятся, например, тексты на русском, ан­глийском и других языках и т.п.

Дата добавления: 2014-01-20