Поняття та елементи часового ряду

Поняття та елементи часового ряду.

План.

2. Побудова і згладжування вихідних кривих.

3. Розроблення та аналіз моделі з адитивними компонентами.

4. Прогнозування за допомогою адитивної моделі.

1. Часовий ряд (або динамічний) – це сукупність даних, які характеризуються зміною деякого показника в часі.

Особливість часових рядів – кожен член ряду являється одночасно результатом минулого розвитку і вихідною передумовою для визначення показників у майбутньому.

Дослідження часового ряду дає можливість виявити закономірності, встановити зв’язок між минулим і сьогоденням, передбачити елементи майбутнього.

Аналіз часових рядів і розроблення прогнозів на майбутні періоди базуються на припущенні інерційності розвитку об’єкта прогнозування.

Розглянемо часові ряди, як сукупність тренду та сезонної варіації.

Тренд (Т) – це загальна зміна значень змінної в часі (закономірність).

Сезонна варіація (S) – циклічні коливання, що повторяються протягом невеликого проміжку часу.

2. Побудова і згладжування вихідних кривих.

У таблиці задано попит на продукцію певного підприємства. Показники попиту залежать від часу, тому розглядаємо їх як часовий ряд.

Таблиця квартального попиту на продукцію

Рік

Квартал

Попит

Нанесемо ці дані на координатне поле та з’єднаємо їх, тобто побудуємо графік залежності об’ємів попиту на продукцію від часу.

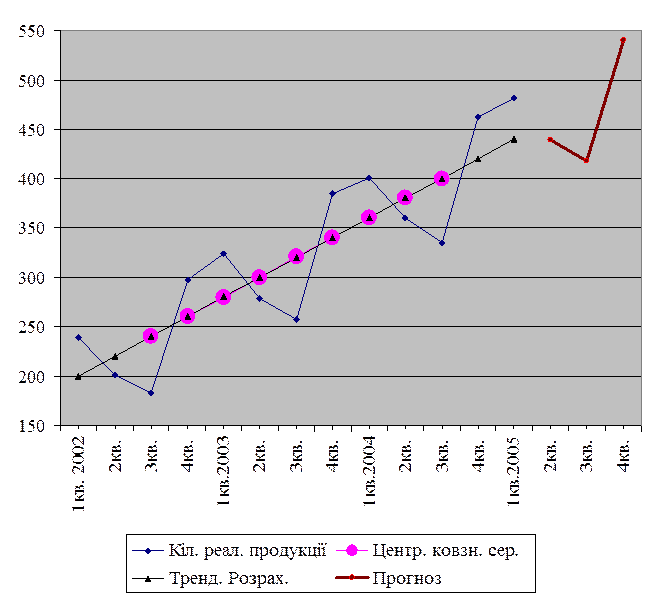
Для виділення можливого тренда (залежності між даними) проведемо згладжування даних, скориставшись методом ковзного середнього.

Алгоритм методу:

1) Обчислюємо суму чотирьох значень елементів стовпця 3 та поміщаємо їх у стовпець 4 на рівні середини цих значень. Повторюємо цю процедуру до кінця стовпця, щоразу зміщуючись (ковзаючи) на одне значення донизу;

2) Кожне значення стовпця 4 ділимо на 4, тобто знаходимо середнє арифметичне та поміщаємо отримані результати у стовпець 5. Зауваження: отримані значення не відповідають ніяким кварталам;

3) Центруємо ці значення шляхом обчислення середнього арифметичного кожної пари, зміщуючись при цьому на кожній ітерації на одне значення вниз по таблиці. Отримані результати поміщаємо у стовпець 6. Ці значення відповідають певним кварталам і являють собою згладжені дані.

№ п\п	Дата (період)	Кількість реалізованої продукції (А)	Разом за 4 квартали	Ковзне середнє значення за 4кв.	Центроване ковзне середнє знач. (Т)
1.	І кв. 2008 р.				----
			---	---
2.	ІІ кв.				----
				229,75
3.	ІІІ кв.				240,4
4.	ІV кв.				260,6
				270,25
5.	Ікв. 2009 р.				279,6
6.	ІІ кв.		·		299,9
				310,75
7.	ІІІ кв.				320,4
8.	ІV кв.				340,3
				350,5
9.	І кв. 2010 р.				360,2
10.	ІІ кв.				379,8
				389,5
11.	ІІІ кв.				399,5
				409,5
12.	ІV кв.				---
			---	---
13.	І кв. 2011				-----

Нанесемо згладжені дані на наш графік. Отримуємо пряму лінію (Рожева пряма).

Аналіз цих даних дає підстави стверджувати про існування лінійного тренда. Проаналізувавши піки – відхилення від прямої, можна виявити певну закономірність їх змін, тобто зробити висновок про їх стабільність у відповідних кварталах, а відтак про наявність адитивних сезонних компонентів.

Таким чином, ми переконались, що фактичні значення попиту на продукцію (А) включають в себе трендові значення (Т) та сезонні компоненти (S). При цьому слід враховувати певну похибку (Е), викликану зовнішніми та внутрішніми чинниками.

3. Розроблення та аналіз моделі з адитивними компонентами.

Моделлю з адитивними компонентами називається така модель, у якій варіація значень змінної в часі найкраще описується через додавання окремих компонентів. Загальний вигляд моделі:

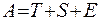, де

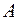– ретроспективні дані (фактичні значення показників за попередні періоди);

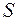– сезонні значення (різні для кожного кварталу);

– тренд (залежність попиту від кварталу);

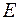– похибка (помилка).

Аналіз моделі з адитивними компонентами складається з наступних етапів:

1) Розрахунок значень сезонних компонентів.

2) Десезоналізація даних.

3) Обґрунтування вигляду і розрахунок параметрів аналітичної функції (тренда).

4) Розрахунок тренда на основі отриманої аналітичної функції.

5) Розрахунок помилок.

6) Встановлення адекватності моделі.

1. Розрахунок значень сезонних компонентів.

Приймаючи отримане центроване ковзне середнє значення як наближений тренд, проведемо оцінку сезонних компонентів: А-Т=S+Е. Результати розрахунків – стовпець 7. для розрахунку сезонних компонентів скористаємось додатковою таблицею.

№ п\п	Дата (період)	Кількість реалізованої продукції (А)		Центроване ковзне середнє знач. (Т)	Оцінка сезонної компоненти (А-Т=S+Е)	Скоригована сезонна компонента (S)	Десезоналізовані дані (А-S=Т+Е)
			4-5
1.	Ікв 2008			----	----	42,6	196,4
2.	ІІ кв.			----	----	-20,7	221,7
3.	ІІІ кв.			240,4	-58,4	-62
4.	ІVкв.			260,6	36,4	40,1	256,9
5.	Ікв 2009			279,6	44,4	42,6	281,4
6.	ІІ кв.			299,9	-21,9	-20,7	298,7
7.	ІІІ кв.			320,4	-63,4	-62
8.	ІVкв.			340,3	43,7	40,1	343,9
9.	Ікв 2010			360,2	40,8	42,6	358,6
10.	ІІ кв.			379,8	-19,8	-20,7	380,7
11.	ІІІ кв.			399,5	-64,5	-62	397,1
12.	ІVкв.			---	---	40,1	429,9
13.	Ікв 2011			-----	-----	42,6	438,4

Додаткова таблиця для розрахунків сезонних компонентів.

Рік	Номер кварталу
І	ІІ	ІІІ	ІV
	---	---	-58,4	36,4
	44,4	-21,9	-63,4	43,8
	40,8	-19,8	-64,5	---
∑	85,2	-41,7	-186,3	80,2
Оцінка сезонної компоненти (середнє арифметичне)	42,6	-20,8	-62,1	40,1	∑ =-0,2
Скоригована сезонна компонента	42,6	-20,7	-62	40,1	∑ = 0

Сума сезонних компонентів повинна дорівнювати нулю, щоб забезпечити нейтралізацію додатних та від’ємних значень. Коригуємо ці значення вручну. Отримані значення заносимо в основну таблицю –стовпець 8.

2. Десезоналізація даних.

Віднімаємо сезонні компоненти від фактичних даних, тобто розраховуємо А- S = Т+Е. Результат – стовпець 9.

3. Обґрунтування вигляду і розрахунок параметрів аналітичної функції (тренда).

Нові оцінки значень тренда, що ще містять помилку, можна використати для побудови моделі основного тренда. Якщо нанести ці значення на графік, можна зробити висновок про існування явного лінійного тренда. Рівняння лінії тренда має вигляд:

Т = а + в · х

де а – характеризує точку перетину з віссю ординат;

в – нахил лінії тренда.

Для визначення параметрів прямої, що найкраще апроксимує тренд, скористаємося методом найменших квадратів.

тут х – порядковий номер кварталу – стовпець 1;

у – значення тренда – стовпець 9 (Т+Е).

Проводимо проміжні обчислення:

Σх = 91; Σх2 = 819; Σу = 4158; Σху = 32747,1; n = 13

Підставивши знайдені значення у відповідні формули отримаємо:

в = 19,978

а = 180,046

Отже, рівняння моделі тренда має наступний вигляд:

Т = 180 + 20*х

4. Розрахунок тренда на основі отриманої аналітичної функції.

№ п\п	Дата (період)	Кількість реалізованої продукції (А)		Скоригована сезонна компонента (S)	Десезоналізовані дані (А-S=Т+Е)	Тренд аналітичний (Т)	Помилки (Е=А-Т-S)
			4-7
1.	І кв. 2008			42,6	196,4		-3,6
2.	ІІ кв.			-20,7	221,7		1,7
3.	ІІІ кв.			-62
4.	ІV кв.			40,1	256,9		-3,1
5.	І кв. 2009			42,6	281,4		1,4
6.	ІІ кв.			-20,7	298,7		-1,3
7.	ІІІ кв.			-62			-1
8.	ІV кв.			40,1	343,9		3,9
9.	І кв. 2010			42,6	358,6		-1,6
10.	ІІ кв.			-20,7	380,7		0,7
11.	ІІІ кв.			-62	397,1		-3
12.	ІV кв.			40,1	429,9		1,9
13.	І кв. 2011			42,6	438,4		-1,6

5. Розрахунок помилок:

Е = А - Т- S (стовпець 9 – стовпець 10)

Результати розрахунку – стовпець 11.

6. Встановлення адекватності моделі.

Для встановлення адекватної моделі розрахуємо середнє абсолютне відхилення (МАД):

МАД =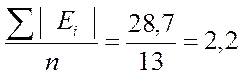

або іншу величину – середню квадратичну помилку (МSЕ)

МSЕ =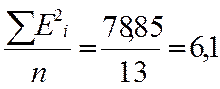

У нашому випадку помилки дуже малі і складають від 1% до 2% від загальних даних (А). Отже тенденція, виявлена за фактичними даними, досить стійка і дозволяє одержати надійні короткострокові прогнози.

4. Прогнозування за допомогою адитивної моделі.

Прогнозні значення по моделі з адитивними компонентами розраховуються таким чином:

Рх =Т +S

де Т – трендові значення, Т = 180 + 20*х;

х – номер періоду прогнозування (кварталу)

S - сезонна компонента: І кв. = 42,6

ІІ кв. = -20,7

ІІІ кв. = -62

ІV кв. = 40,1

Р14 = 180 + 20* 14 + (-20,7) = 460 – 20,7 =439,3

Р15 = 180 + 20 * 15 + (-62) = 480 – 62 = 418

Р16 = 180 + 20 * 16 + 40,1 = 540,1

Наносимо на графік отримані значення. Слід зазначити, що розраховані прогнозні значення містять похибку 1-2%. Розраховані показники матимуть місце за умови, що тенденція, виявлена за ретроспективними даними, поширюється і на майбутній період. Чим більш віддаленим буде період прогнозування, тим менш точним буде прогноз.

Дата добавления: 2014-01-11