Эффект Зеемана

В магнитном поле уровень (n, L, S, J) расщепляется на 2J+1 компонент с энергиями

E(J,m) = g μ B m. μ - магнетон Бора, g - фактор Ланде, В - напряженность магнитного поля, m - магнитное квантовое число m = ± 1, ± 2... Фактор Ланде зависит от L и S

(1.20)

Если S=0, то J=L и g = 1.Если L=0, то J=S и g = 2. Если S=1/2, L=1, J=3/2 то g = 1.2

Правила отбора ΔJ =0, ± 1 Δm = 0, ± 1.

Если значения факторов Ланде для верхнего и нижнего уровней совпадают, эффект Зеемана проявляется в виде расщепления линии на 3 компоненты в соответствии с Δm.

Исторически этот случай был открыт первым и поэтому называется "нормальный эффект Зеемана". Одна компонента несмещенная по частоте (Δm = 0) называется π - компонентой и две σ - компоненты на частотах ω = ω₀ ± ω_се. При наблюдении поперек магнитного поля наблюдаются 3 линии: две σ - компоненты поляризованы ^ магнитному полю, а π - компонента - параллельно полю. При наблюдении вдоль магнитного поля π - компонента не видна, а две σ - компоненты поляризованы по кругу в противоположных направлениях.

Если значения факторов Ланде для верхнего и нижнего уровней не равны, спектр состоит из множества компонент, а разность частот между компонентами отличается от ω_се. Это - аномальный эффект Зеемана.

Для измерения магнитного поля предпочтительнее выбрать переход с нормальным эффектом Зеемана при наблюдении поперек магнитного поля. В этом случае величина расщепления (1.21)

Здесь λ в мкм, В в Гауссах, Δλ в Å. В поле В = 10⁴ Гаусс для света с λ = 0.5 мкм величина Зеемановского расщепления Δλ = 0.12 Å. Это сравнимо с доплеровским уширением. Поэтому расщепление проявляется в виде дополнительного уширения на фоне доплеровского. Чтобы выделить зеемановскую часть находят разность π - σ между шириной компонент с поляризацией вдоль и поперек поля. Доплеровское уширение у них одинаково, так что в разности ширин эффект Зеемана проявляется в чистом виде.

Динамический Штарковский сдвиг "motional Stark Effect"

В современных термоядерных экспериментах для нагрева плазмы широко используются пучки быстрых нейтральных атомов водорода с энергией до 1 МэВ. Их можно использовать для измерения величины и направления магнитного поля. При движении атома в магнитном поле он испытывает действие индуцированного электрического поля

. Действие электрического поля проявляется через эффект Штарка. Измерив величину Е можно найти компоненту В перпендикулярную к скорости атомов, а из нее - полоидальную компоненту магнитного поля. Знание В_пол очень важно для анализа поведения плазмы, так как ею определяется значение коэффициента запаса устойчивости

.

Для водорода величина Штарковского сдвига для уровня n будет

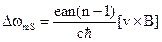(1.21)

Величина динамического штарковского сдвига сравнивается с зеемановским уже при энергии атомов в пучке ~ 1 КэВ. А при энергии 100 КэВ - на порядок больше. Поэтому такой метод измерения В предпочтительнее.

Дата добавления: 2014-01-20