Размещения

Допустим, n независимых друг от друга величин а₁,а₂,…,а_n, для которых порядок расположения имеет значение, могут принимать равное количество значений m. Например, разряды десятичного числа, вносящие в него различный вклад, могут независимо принимать m=10 значений от 0 до 9.

Данный способ расположение объектов называют размещением из n по m и обозначают U(n, m) либо . Поскольку значения величин могут повторяться при размещении на различных местах, то данный случай также можно назвать размещением с повторениями.

Поскольку для каждой величины а₁, а₂,…, а_n число вариантов значения не зависит от остальных и равно m, то, применяя (n-1) раз правило умножения, получим общую формулу для расчета : .

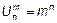Многие практические задачи оценки количества комбинаторных объектов сводятся к подсчету размещений с повторениями.

Пример 4. Найти количество N попарно различных 3-значных десятичных чисел для двух случаев:

1) когда в начале записей разрешены незначащие нули, и

2) когда в записях незначащие нули недопустимы.

Решение.1) Если нет ограничения на использование нулей, то в каждом разряде чисел может быть одна из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Получаем задачу размещения с параметрами: n=3, k=10. Следовательно, .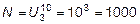

2) Если использование незначащих нулей в начале записи чисел недопустимо, то в каждом из двух младших разрядов, как и в случае 1), может быть одна из 10 цифр, а в старшем разряде только одна из 9: (1, 2, 3, 4, 5, 6, 7, 8, 9). Поскольку цифры в разрядах размещаются независимо, то общее количество различных чисел в данном случае составит N=9×10²=900.

Ответ. 1) 1000; 2) 900.

Дата добавления: 2014-01-20