Перестановки и размещения без повторений групп одинаковых объектов

Пусть на n местах располагают n объектов, которые, в отличие от обычных перестановок, образуют s групп одинаковых объектов. В каждой группе i (1£i£s) число объектов обозначим k_i. При этом k_i³1, k₁+k₂+ …+k_s=n).

Тогда общее количество различных сочетаний объектов на n местах равно

С качественной точки зрения перемена местами одинаковых объектов не изменяет набор объектов.

Пример 7. Определить число всех различных возможных со­общений длиной в 13 букв, в которых содержатся 4 буквы "a", 2 бук­вы "б", 1 буква "и", 6 букв "р".

Решение. Задача сводится к определению числа вариантов перестановки, содержащей группы одинаковых объектов. Параметры ее: s=4, k₁=4, k₂=2, k₃=1, k₄=6. По общей формуле число данных сообщений равно:

N=13!/(4!×2!×1!×6!)=(6!×7×8×9×10×11×12×13)/(6!×2!×4!)=180180.

Ответ. 180180.

Пример 8. В финал олимпиады по информатике вышло 10 участников. Определить число всех различных возможных вариантов победителей и призеров олимпиады, если организаторы плани­руют присудить 1 первое, 2 вторых и 3 третьих места, остальным присвоить звание призеров. Порядок участников, занявших одина­ковое место, не важен.

Решение. Задача также сводится к определению количеств перестановок, в которых есть группы одинаковых объектов - участники, занявшие одинаковое (с точки зрения награды) место. Парамет­ры ее: s=4 (среди победителей и призеров 4 различных группы), k₁=1 (первое место), k₂=2 (второе место), k₃=3 (третье место), k₄=4 (призеры), n=10. По общей формуле число возможных вариантов победителей и призеров:

N=10!/(1!×2!×3!×4!)=(10×9×8×7×6×5)/(2!×3!)=10×9×4×7×5=12600.

Ответ. 12600.

Если число размещаемых объектов k меньше числа мест n (k<n), то для расчета их общего числа используется аналогичная формула

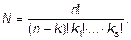
Пример 9. В 8 пронумерованных лунках размещают 2 одинаковых белых и 3 одинаковых черных шара. Найти общее число вариантов размещения.

Решение. В задаче две группы одинаковых объектов, в которых числа k₁=2, k₂=3. Общее число размещаемых шаров k=k₁+k₂= =2+3=5. Поэтому задача сводится к определению числа размещений без повторений из 8 по 5 с двумя группами одинаковых объектов (k₁=2, k₂=3):

Ответ. 560.

Дата добавления: 2014-01-20