Единицы измерения времени выполнения алгоритма

Для этой цели можно просто воспользоваться общепринятыми единицами измерения времени — секундой, миллисекундой и т.д. и с их помощью оценить время выполнения программы, реализующей рассматриваемый алгоритм. Однако у такого подхода существуют явные недостатки, поскольку результаты измерений будут зависеть от:

¦ быстродействия конкретного компьютера;

¦ тщательности реализации алгоритма в виде программы;

¦ типа компилятора, использованного для генерации машинного кода;

¦ точности хронометрирования реального времени выполнения программы.

Поскольку перед нами стоит задача измерения эффективности алгоритма, а не реализующей его программы, мы должны воспользоваться такой системой измерений, которая бы не зависела от приведенных выше посторонних факторов.

Один из возможных способов решения этой проблемы состоит в подсчете того, сколько раз выполняется каждая операция алгоритма. Однако подобный подход слишком сложен и чаще всего не нужен. Поэтому мы должны составить список наиболее важных операций, выполняемых в алгоритме, называемых основными, или базовыми операциями {basic operation), определить, какие из них вносят наибольший вклад в общее время выполнения алгоритма, и вычислить, сколько раз эти операции выполняются. Как правило, составить список основных операций алгоритма не трудно. Обычно в него включают наиболее длительные по времени операции, выполняемые во внутреннем цикле алгоритма. Например, в большинстве алгоритмов сортировки используется метод сравнения двух элементов (ключей) списка, который сортируется. Для подобного типа алгоритмов основной является операция сравнения ключей. В качестве еще одного примера рассмотрим алгоритмы перемножения матриц и вычисления значения многочлена. В них используются две основные операции: умножение и сложение. На большинстве компьютеров команда умножения двух целых чисел выполняется намного дольше, чем сложение. Поэтому она является безусловным кандидатом на включение в список основных операций.

Таким образом, для анализа временной эффективности алгоритмов этот показатель будет оцениваться по количеству основных операций, которые должен выполнить алгоритм при обработке входных данных размера n.

Рассмотрим один важный пример. Предположим, что с_ор — время выполнения основной операции алгоритма на конкретном компьютере, а С (n) — количество раз, которые эта операция должна быть выполнена при работе алгоритма. Тогда время выполнения программной реализации этого алгоритма на данном компьютере T(n) можно приблизительно определить по следующей формуле: 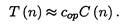Разумеется, эту формулу нужно использовать очень аккуратно. В значении счетчика С(n) не учитывается количество выполняемых алгоритмом операций, не относящихся к основным. Кроме того, обычно значение этого счетчика можно определить только приблизительно. Более того, значение константы С_ор также можно определить лишь приблизительно и оценить ее точность весьма непросто. Тем не менее, эта формула дает приемлемую оценку времени выполнения алгоритма для небесконечно больших и небесконечно малых значений n. Она также позволяет ответить на вопросы: во сколько раз быстрее будет работать реализация данного алгоритма на компьютере, быстродействие которого больше нашего в 10 раз?

В самом деле, для достаточно больших n справедлива следующая формула:

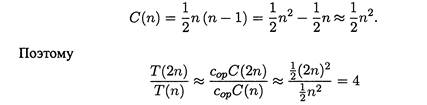
Этому в процессе анализа эффективности при достаточно больших размерах входных данных не учитывают постоянные множители, а сосредотачиваются на оценке порядка роста (order of growth) количества основных операций с точностью до постоянного множителя.

Дата добавления: 2014-01-20