Прогнозирование на основе уравнений тренда

В специальной литературе по статистическим методам прогнозирования уравнения тренда нередко называют моделями кривых роста, так как различные виды уравнений тренда отражают различные закономерности развития (роста) тех или иных процессов во времени. Процедура разработки прогноза с использованием трендовых моделей включает в себя несколько этапов:

1) Выбор одной или нескольких моделей, графическое изображение которых соответствует характеру изменения временного ряда;

2) Оценка параметров выбранных моделей (уравнений тренда);

3) Проверка адекватности выбранных моделей прогнозируемому процессу и окончательный выбор вида уравнения тренда;

4) Расчет точечного и интервального прогноза.

В настоящее время в специальной литературе описано несколько десятков кривых роста, многие из которых широко применяются для выравнивания динамических рядов экономических процессов. Кривые ролста обычно делят на три типа, в зависимости от того, какой тип динамики они описывают.

К I типу относят функции с монотонным развитием и отсутствием пределов роста. Эти условия справедливы для многих экономичесикх показателей, например, для большинства натуральных показателей промышленного производства.

Ко II типу относят кривые, описывающие процесс, который может иметь пределы роста в рассматриваемом периоде. С такими процессами часто сталкиваются в демографии, при изучении потребностей в товарах и услугах (в расчете на душу населения), при исследовании эффективности использования ресурсов и т.д. Примерами показателей, для которых могут быть указаны пределы роста, является потребление продуктов питания на душу населения, расход удобрений на единицу площади и др.

Математические функции, относящиеся к данному типу, часто называют «кривыми насыщения». Если «кривые насыщения» имеют так называемые «точки перегиба», то они относятся к III типу – S – образным кривым. Эти кривые описывают как бы два последовательных лавинообразных процесса (когда процесс зависит от уже достигнутого уровня): один с ускорением развития, другой с замедлением.

S – образные кривые находят применение в демографических исследованиях, в страховых расчетах, при решении задач прогнозирования научно-технического прогресса, при определении спроса на новый вид продукции.

Вопрос о выборе формы кривой является одним из основных при выравнивании динамического ряда.

К I типу кривых относятся, прежде всего, различные виды полиномов (линейная функция, парабола второго порядка, парабола третьего порядка и полиномы более высоких степеней).

Коэффициенты полиномов невысоких степеней можно интерпретировать в зависимости от содержания исходного динамического ряда. Например, параметр a1 трактуется как скорость роста, параметр a2 – как ускорение (изменение скорости), параметр a3 – как изменение ускорения, а константа a0 – начальный уровень процесса при t=0.

Использовать для моделирования тренда полиномы более высоких степеней не целесообразно, поскольку полученные таким образом аппроксимирующие функции будут отражать случайные отклонения, что противоречит смыслу моделируемой тенденции.

Обычно полином первой степени (линейный тренд) используется для моделирования процессов, развивающихся равномерно, полином второй степени (квадратический тренд) применяется в случаях если процесс развивается равноускоренно (т.е. имеется равноускоренный рост или, наоборот, равноускоренное снижение уровней ряда).

Для экспоненциальных кривых, в отличие от полиномов, характерна зависимость приростов от величины самой функции. Поэтому эти кривые хорошо описывают процессы, имеющие «лавинообразный» характер. К такому типу кривых относятся показательная и степенная функции, а также так называемая логарифмическая парабола, типа:

y_t = a b^t c ^t2

Путем логарифмирования это выражение преобразуется в параболу:

log y_t = log a+t log b +t² log c

Полученная функция имеет линейный вид, поэтому ее параметры легко находятся методом наименьших квадратов.

Все эти кривые используются для описания процессов «без насыщения».

Если же процесс имеет некие «пределы роста» или «пределы насыщения» (как, например, расход ограниченного запаса ресурсов или покупательский спрос на некоторые товары), то этот процесс следует описывать кривой, имеющей некоторую асимптоту (отличную от нуля), т.е. кривой II типа.

Примером такой кривой является модифицированная экспонента:

y_t = K +a b^t

для которой прямая y=K является горизонтальной асимптотой. При моделировании экономических процессов чаще всего приходится иметь дело с кривой, у которой a<0, b<1. В этом случае рост уровней происходит с замедлением и стремится к некоторому заданному пределу.

На рис.13.1. приведен график модифицированной экспоненты y= 12-2×(0.9)^t

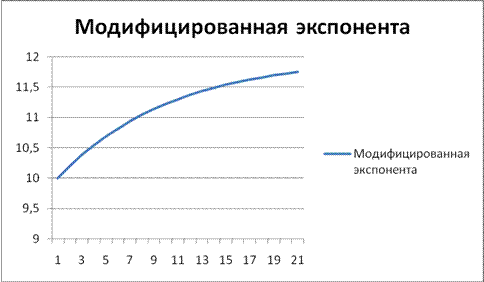
Рис. 13.1. График функции y = К + ab^t

При решении экономических задач часто можно определить значение асимптоты, исходя из свойств прогнозируемого процесса (например, коэффциент использования оборудования не может превышать 1). В других случаях значение асимптоты задается экспертным путем.

При заданной асимптоте (пределе роста) K* другие параметры этой функции определяются методом наименьших квадратов, так как модифицированная экспонента приводится к линейному виду путем логарифмирования:

log (y_t – K*) = log a+t log b

В случае, если воздействие некоторого ограничивающего фактора начинает сказываться только после некоторого периода ускоренного роста, т.е. после «точки перегиба», до которой процесс развивался по экспоненциальному закону, для моделирования таких процессов используют функции III типа – S-образные кривые.

Наиболее известными из них являются кривая Гомперца и логистическая кривая или кривая Перла-Рида. Уравнения этих функций были приведены на лекции №9.

Логистическая функция имеет вид:

y = ;

кривая Перла-Рида:

y = ;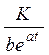

кривая Гомперца

y =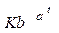

Основная разница между графиками этих функций в том, что кривая Гомперца не симметрична, а логистическая кривая и кривая Перла-Рида – симметричны относительно точки перегиба.

Параметры этих функций после их логарифмирования также рассчитываются методом наименьших квадратов.

Дата добавления: 2014-01-20