Метод гармонической линеаризации

Метод гармонической линеаризации (гармонического баланса [9, с.228]) позволяет определить условия существования и параметры возможных автоколебаний в нелинейных САУ. Автоколебания определяются предельными циклами в фазовом пространстве систем. Предельные циклы разделяют пространство (в общем случае - многомерное) на области затухающих и расходящихся процессов. В результате расчета параметров автоколебаний можно сделать заключение о их допустимости для данной системы или о необходимости изменения параметров системы.

Метод позволяет:

- определить условия устойчивости нелинейной системы;

- найти частоту и амплитуду свободных колебаний системы;

- синтезировать корректирующие цепи, для обеспечения требуемых параметров автоколебаний;

- исследовать вынужденные колебания и оценивать качество переходных процессов в нелинейных САУ.

Метод основан на замене нелинейного элемента его линейным эквивалентом. Эквивалентность достигается для движения системы близкого к гармоническому.

Условия применимости метода гармонической линеаризации.

1) При использовании метода предполагается, что линейная часть системы устойчива или нейтральна.

2) Сигнал на входе нелинейного звена близок по форме к гармоническому сигналу. Это положение требует пояснений.

На рис.1 представлены структурные схемы нелинейной САУ. Схема состоит из последовательно соединенных звеньев: нелинейного звена y=F(x) и линейно-

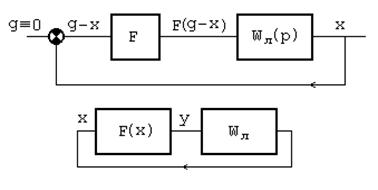
Рис.1

го, которое описывается дифференциальным уравнением

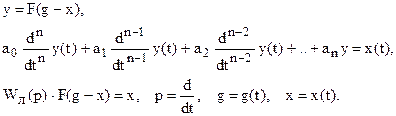
При y = F(g - x) = g - x получим уравнение движения линейной системы.

Рассмотрим свободное движение, т.е. при g(t) º 0. Тогда,

В случае, когда в системе существуют автоколебания, свободное движение системы является периодическим. Непериодическое движение с течением времени оканчивается остановкой системы к некотором конечном положении (обычно, на специально предусмотренном ограничителе).

При любой форме периодического сигнала на входе нелинейного элемента сигнал на его выходе будет содержать кроме основной частоты высшие гармоники. Предположение о том, что сигнал на входе нелинейной части системы можно считать гармоническим, т.е., что

x(t)@ a×sin(wt),

где w=1/T, T - период свободных колебаний системы, равносильно предположению о том, что линейная часть системы эффективно фильтрует высшие гармоники сигнала y(t) = F(x (t)).

В общем случае при действии на входе нелинейного элемента гармонического сигнала x(t) сигнал на выходе может быть преобразован по Фурье:

Коэффициенты ряда Фурье

.

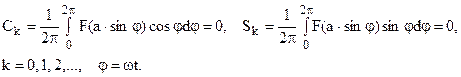Для упрощения выкладок положим C₀ =0, т.е., что функция F(x) симметрична относительно начала координат. Такое ограничение не обязательно и сделано анализа. Появление коэффициентов C_k ¹ 0 означает, что, в общем случае нелинейное преобразование сигнала сопровождается и фазовыми сдвигами преобразуемого сигнала. В частности, это имеет место в нелинейностях с неоднозначными характеристиками (с различного рода гистерезисными петлями), причем как запаздывание так и, в некоторых случаях, опережение по фазе.

Предположение об эффективной фильтрации означает, что амплитуды высших гармоник на выходе линейной части системы малы, то есть

Выполнению этого условия способствует то, что во многих случаях амплитуды гармоник уже непосредственно на выходе нелинейности оказываются существенно меньше амплитуды первой гармоники. Например, на выходе идеального реле при гармоническом сигнале на входе

y(t)=F(с×sin(wt))=a×sign(sin(wt))

четные гармоники отсутствуют, а амплитуда третьей гармоники в три раза меньше амплитуды первой гармоники

Сделаем оценку степени подавления высших гармоник сигнала в линейной части САУ. Для этого сделаем ряд предположений.

1) Частота свободных колебаний САУ приблизительно равна частоте среза ее линейной части. Отметим, что частота свободных колебаний нелинейной САУ может существенно отличаться от частоты свободных колебаний линейной системы так, что это допущение не всегда корректно [9].

2) Показатель колебательности САУ примем равным M=1.1.

3) ЛАХ в окрестностях частоты среза (w_с) имеет наклон -20 дБ/дек. Границы этого участка ЛАХ связаны с показателем колебательности соотношениями [2]

4) Частота w_max является сопрягающей с участком ЛФХ, так что при w > w_max наклон ЛАХ не менее минус 40 дБ/дек.

5) Нелинейность - идеальное реле с характеристикой y = sign(x) так, что на ее выходе нелинейности будут присутствовать только нечетные гармоники.

Частоты третьей гармоники w₃ = 3w_c , пятой w₅ = 5w_с,

lgw₃ = 0.48+lgw_c,

lgw₅ = 0.7+lgw_c.

Третья гармоника отстоит от частоты среза на 0.48 декады, пятая - на 0.7 декады.

Частота w_max = 1.91w_с , lgw_max = 0.28+lgw_c. Сопрягающая частота отстоит от частоты среза на 0.28 декады.

Уменьшение амплитуд высших гармоник сигнала при их прохождении через линейную часть системы составит для третьей гармоники

L₃ = -0.28×20-(0.48-0.28)×40 = -13.6 дБ, то есть в 4.8 раза,

для пятой - L₅ = -0.28×20-(0.7-0.28)×40 = -22.4 дБ, то есть в 13 раз.

Следовательно, сигнал на выходе линейной части окажется близким к гармоническому

.

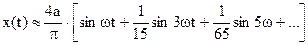Идея гармонической линеаризации состоит в замене нелинейного звена линейным звеном. Параметры линейного звена выбираются таким образом, чтобы при заданной амплитуде гармонического сигнале на входе нелинейного элемента амплитуда первой гармоники на выходе обоих звеньев были одинаковы.

Это эквивалентно предположению, что система является низкочастотным фильтром.

Дата добавления: 2014-01-20