Показатели ремонтопригодности

Показатели ремонтопригодности характеризуют процесс восстановления таких систем (их работоспособного состояния).

К числу таких показателей относят следующие:

1) P _в (t) – вероятность восстановления работоспособного состояния объекта за время t.

Математически эта вероятность определяет вероятность того, что время восстановления работоспособного состояния τ _в будет меньше наперед заданной величины t, то есть:

P_в(t) = P {τ_в< t}

где t – требуемое время восстановления объекта, которое определяется технической документацией или представляет собой реальное время, которое может быть затрачено на восстановление.

Эта вероятность P _в (t) представляет собой интегральную функцию распределения случайной величины τ _в.

Статистическое значение вероятности P _в (t) определяется следующим образом:

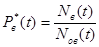, (1)

где N _в (t) – число восстановленных объектов за время t;

N _ов (t) – число отказавших объектов, которые поставлены в очередь на восстановление.

2) ƒ _в (t) – плотность вероятности восстановления работоспособного состояния объекта (частота восстановления; плотность (закон) распределения времени восстановления).

Данный показатель является дифференциальной функцией распределения случайной величины τ _в. Поэтому она определяется как производная от интегральной функции распределения:

, (2)

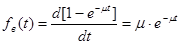, (3)

где μ – интенсивность восстановления объекта.

Определим связь между характеристиками P _в (t), ƒ _в (t) и μ.

Из формулы (2) можно записать:

(4)

Проинтегрируем обе части выражения (4):

,

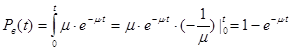
Таким образом P _в (t) определяется:

(5)

Геометрически P _в (t) представляет собой возрастающую экспоненту:

Статистическое значение плотности вероятности отказов будет определяться по следующей формуле:

, [1/ч] (6)

где N _в (Δt) – число объектов, восстанавливаемых на интервале времени Δt;

N _ов (t) – число объектов, требующих восстановления на интервале времени t.

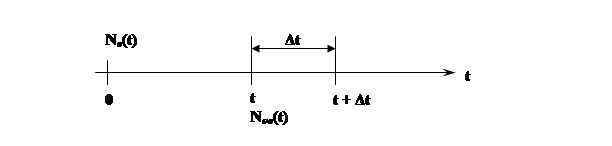
3) μ(t) – интенсивность восстановления работоспособного состояния объекта за время t.

Она определяется как условная плотность вероятности восстановления объекта в момент времени t при условии, что до этого момента времени t восстановление объекта не произошло.

.

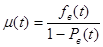В период нормальной эксплуатации объекта (то есть для экспоненциального закона восстановления) характеристика μ(t) является величиной постоянной μ(t) = μ = const. Точное значение характеристики μ определяется по следующей формуле:

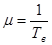, [1/ч] (7)

где Т _в – среднее время восстановления работоспособного состояния системы.

Статистически интенсивность восстановления μ определяется по следующей формуле:

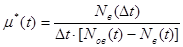, (8)

где N _ов (t) – N _в (t) – число невосстановленных объектов за время t.

4) Т _в – среднее время восстановления объекта.

Оно определяется как математическое ожидание случайной величины τ _в:

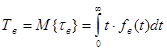, (9)

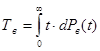. (10)

Интеграл (10) приведем к табличному виду и запишем его:

∫UdV = UV - ∫VdU

Введем следующие обозначения: t = U, dP_в(t) = dV, dt = dU, V = P_в(t). Тогда формулу (10) запишем в виде:

(11)

В формуле (11) произведение t·P _в (t) можно заменить единицей, так как при t→ ∞ вероятность P _в (t→ ∞) будет стремиться быстрее, чем t будет стремиться к ∞. Поэтому точное значение средней наработки до отказа будет равно:

. (12)

Определим связь между характеристиками Т _в и μ. Для этого воспользуемся формулой (11), в которую подставим вместо вероятности Р _в (t) ее значение 1- е ^-μ·t:

.

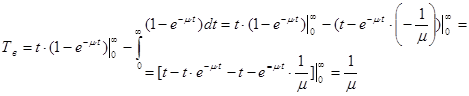При t→ ∞ произведение t·е ^-μ·t можно заменить нулем, так как экспонента е ^-μ·t будет стремиться к нулю быстрее, чем t будет стремиться к бесконечности. Таким образом:

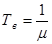(13).

По результатам испытаний приближенное значение характеристики Т _в определяется по формуле:

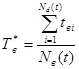, (14)

где t _вi – суммарное время, затраченное на восстановление работоспособного состояния i - ого испытуемого объекта.

Для восстановления систем число восстановлений равно числу отказов, и каждый испытуемый объект может иметь за время t несколько отказов. Поэтому характеристику Т^* _в можно вычислять по следующей формуле:

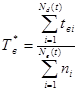, (15)

где n_i – это суммарное число отказов, возникших у i – ого объекта за время испытаний t.

Формула (15) определяет среднее время восстановления, затрачиваемое на один отказ на один восстановленный объект. В формуле (15) верхние пределы в суммах можно заменить общим числом объектов N₀, поставленных на испытание. Поэтому для неотказавших объектов соответствующие значения t _вi и n_i можно заменить нулем. Тогда:

. (16)

Формула (16) определяет характеристику Т _в ^* как среднее время, затрачиваемое на восстановление одного отказа в одном объекте.

Дата добавления: 2014-01-20