Тема 4. Расчет надежности дискретных невосстанавливаемых систем с дробной кратностью резервирования

Для дискретных устройств кроме постоянных отказов присущи самоустраняющиеся отказы (сбои). Если не принимать особых способов борьбы со сбоями, то дискретная система может оказаться неработоспособной. В качества таких способов борьбы со сбоями используются:

1) помехоустойчивое кодирование передаваемых сообщений;

2) структурное резервирование дискретных устройств с дробной кратностью и с использованием мажоритарных элементов (элементов голосования по большинству). Эти элементы голосования часто называют восстанавливающими органами.

Второй способ используется не только для борьбы со сбоями, но и для борьбы с постоянными отказами. Изобразим в общем виде структурную схему резервированной системы с дробной кратностью (рис. 1).

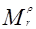- мажорирование из r входов по ρ;

r – общее число дискретных устройств;

ρ – число дискретных устройств, которые должны быть работоспособными, чтобы на выходе Y двоичная последовательность совпадала с входной последовательностью X. Поэтому параметр ρ называют порогом голосования мажоритарного элемента;

r-ρ – число объектов, которые могут отказать в системе без нарушения ее работоспособности.

Поэтому кратность резервирования для таких систем определяется по следующей формуле:

.

Если r = 3, то используется элемент голосования , то есть из трех дискретных устройств может отказать только одно, при этом на выходе Y будут только истинные значения. При ρ = 2 m = 0,5.

Используются также элементы голосования , .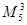

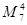Пусть мы имеем систему, у которой значения параметров такие: r = 3, ρ = 2. Сигнал Y на выходе системы для схемы рис.1 можно записать в следующем виде:

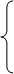
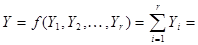1, если 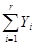≥ρ,

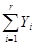0, если <ρ.

Расчет надежности систем с дробной кратностью резервирования мы будем проводить с использованием непрерывной модели отказов, то есть случайной величиной является наработка до отказа r, а вероятности безотказной работы дискретных устройств имеют экспоненциальный закон, то есть P_i(t) = e^-λ_i^·t, i=1,2,3, где λ_i – интенсивность отказа i-ого дискретного устройства.

Составим таблицу состояний дискретных устройств ДУ1 ÷ ДУ3 и состояний системы.

Таблица 1 – Таблица состояний дискретных устройств ДУ1 ÷ ДУ3 и состояний системы.

Номер состояния	Состояние ДУ1	Состояние ДУ2	Состояние ДУ3	Состояние cистемы S	Вероятности cобытий Ri(i=0÷7)
					(1-р1)(1-р2)(1-р3)
					(1-р1)(1-р2)р3
					(1-р1)р2(1-р3)
					(1-р1)р2р3
					р1(1-р2)(1-р3)
					р1(1-р2)р3
					р1р2(1-р3)
					р1р2р3

Состояние любого i-ого дискретного устройства S_ДУi будет равно единице (S_Дуi = 1), если данное дискретное устройство находится в работоспособном состоянии. S_Дуi = 0, если соответствующее дискретное устройство отказало.

Аналогично состояние резервированной системы S = 1, если она находится в работоспособном состоянии, и S = 0, если эта система находится в состоянии отказа. Отказ резервированной системы будет в том случае, если откажут два или все три дискретных устройства.

Вероятность безотказной работы резервированной системы будет определяться суммой вероятностей нахождения системы в работоспособных состояниях.

Из таблицы 1 можно записать:

P_c(t) = R₃ + R₅ + R₆ + R₇ = (1-p₁)p₂p₃ + p₁(1-p₂)p₃ + p_{1 ·}p₂(1-p₃) + p₁ p₂p₃

где р_i = p_i(t)= e^-λ_i^t (i=1 ÷ 3) – вероятности безотказной работы i-ого дискретного устройства;

λ_i – интенсивность отказа i-ого дискретного устройства;

Q_c(t)=1 – P_c(t),

.

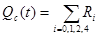Структурные схемы мажоритарных элементов или элементов голосования могут быть построены двумя способами, в частности, если r=3 и ρ=2, то эти два способа построения мажоритарных элементов можно реализовать с помощью следующих формул:

1) Y = y₁y₂ v y₂y₃ v y₁y₃; (1)

2) Y = (y₁ v y₂)(y₂ v y₃)(y₁ v y₃). (2)

Структурные схемы мажоритарных элементов в соответствии с формулами (1) и (2) будут иметь следующий вид (рис.1 и рис.2):

Выходной сигнал на рис.1 и рис.2:

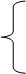1, если 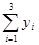≥ ρ =2,

0, если 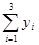<ρ =2.

Если из трех символов два будут равны нулю, то на выходе системы будет ноль.

Дата добавления: 2014-01-20