Искажения в картографических проекциях

Понятие о картографических проекциях

Картографическая проекция – математически определенное отображение поверхности земного эллипсоида на плоскости. При этом на карте передаются положения и очертания картографируемых объектов, а также сетка меридианов и параллелей. Закон, определяющий картографическую проекцию, может быть выражен:

1. Ее уравнениями;

2. Указанием графического построения;

3. Таблицей координат и другими способами.

Уравнением картографической проекции называют два уравнения, определяющие связь между координатами точек на карте и соответствующих точек на поверхности эллипсоида.

Координатные сетки – это картографическая, прямоугольная, километровая и другие сетки. Картографическая сетка – есть изображение параллелей и меридианов на карте.

Прямоугольная сетка на карте – это координатная сетка в системе плоских прямоугольных координат в данной картографической проекции.

Километровая сетка – это координатная сетка, линии которой проведены на карте через интервалы, соответствующие определенному числу километров. Точки пересечения линий координатной сетки на карте называют узловыми точками.

Карте присущи искажения длин, площадей, углов и форм.

1. Искажения длин выражаются в том, что масштаб длин на карте изменяется при переходе от одной точки к другой, а также при изменении направления в данной точке;

2. Искажения площадей возникают из-за того, что масштаб площадей в разных местах карты различен;

3. Искажения углов заключаются в том, что углы между направлениями на карте не равны соответствующим углам на земной поверхности. Углы между линиями географических объектов искажены, что приводит к нарушению форм самих объектов;

4. Искажения форм заключаются в том, что фигуры объектов на карте не подобны соответствующим географическим фигурам на местности.

Все виды искажений на карте связаны друг с другом, и изменение одного из них влечет за собой изменения других. Особый характер имеет связь между искажениями площадей и углов. Уменьшение одного из них влечет увеличение другого. Нет карт без искажений, однако имеются карты, в которых либо отсутствуют искажения углов, либо отсутствуют искажения площадей, либо искажения углов и площадей как бы уравновешены.

Показателем искажений длин в данной точке по данному направлению является частный масштаб длин µ, выражаемый в долях главного масштаба. Он может быть больше главного (например, 2,32) и меньше его (например, 0,81). Масштаб µ меняет свою величину в данной точке в зависимости от направления. По одному из направлений в данной точке масштаб длин имеет наибольшее, а по другому – наименьшее значение. Эти направления взаимно перпендикулярны, и их называют главными направлениями. Наибольший масштаб длин обозначим через 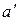, а наименьший – Особо выделяют частные масштабы длин по меридианам – и по параллелям – (рис. 2.1.). Иногда в качестве показателя искажения длин берут не значения масштабов а их отличия от единицы, то есть 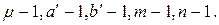Этот показатель называют относительным искажением и часто выражают в процентах. В некоторых случаях искажения длин оценивают логарифмом частного масштаба длин, например, Если искажений в данной точке нет, то есть то

Показатели искажений площадей принимают частный масштаб площадей выражаемый в долях главного масштаба площадей. Он также может быть больше или меньше единицы. Вместо используют относительный показатель часто выражаемый в процентах и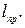

Рис. 2.1. Элементарный сфероидический треугольник

Величина искажения угла в данной точке карты зависит от направления сторон угла. Поэтому в качестве показателя искажения углов на карте принято наибольшее искажение 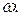Наименьшее искажение углов в данной точке карты всегда равно нулю. В любой точке карты всегда имеется угол, который изображается без искажений. Это угол между главными направлениями, который всегда равен 90°. Кроме 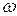используется показатель характеристики угла между изображениями на карте линий меридианов и параллелей. Этот угол на карте в общем случае не равен углу между меридианом и параллелью и обозначается (тета), а его отклонение от значения угла между меридианом и параллелью на поверхности относимости, характеризующее его искажение, – 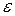(ипсилон). На шаре или эллипсоиде вращения меридианы и параллели пересекаются под прямыми углами. Поэтому для указанных поверхностей относимости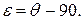

Искажения форм (как и углов) являются следствием того, что частный масштаб длин по разным направлениям различен. Поэтому отношение 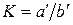характеризует искажение форм. Чем больше величина 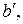тем сильнее вытянут в направлении 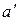контур на карте. Показатель K характеризует искажение форм бесконечно малых фигур. Для конечных фигур он является приближенным показателем. Он достаточно хорошо отражает искажение форм относительно малых географических объектов, таких, как Крымский полуостров, остров Тасмания и даже Кольский полуостров. Но для крупных объектов, таких как материки и даже как остров Гренландия, он неточен. Используют и другие показатели, например:

Показатель 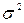учитывает как искажения площадей, так и искажения форм (углов). Если его рассматривать как вектор в системе координат (рисунок 11), то угол 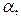определяющий поворот этого вектора, вычисляется как:

Он характеризует соотношения площадей и искажений углов.

При нет искажений углов, при отсутствии искажений площадей при искажения форм и площадей уравновешены, то есть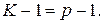

Наиболее точно все виды искажений в данной точке карты можно представить в виде эллипса искажений (рисунки 12 и 13). Эллипс искажений в данной точке карты изображает бесконечно малый круг на поверхности относимости. Его полуоси равны величинам 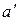и 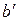они ориентированы по главным направлениям. Радиус вектор эллипса искажений может быть ориентирован по любому направлению и определяет частый масштаб длин по этому направлению. Форма эллипса характеризует искажения углов и форм – они искажены тем больше, чем больше эллипс отличается от окружности. Площадь эллипса пропорциональна искажению площадей и тем она больше, чем больше искажены площади. Желая показать на карте эллипсы искажений, условно принимают радиусы бесконечно малых окружностей на шаре или эллипсоиде равными конечной величине (например, 5 мм в масштабе карты). Тогда все показываемые на карте эллипсы также примут конечные величины.

Их можно сравнивать и сопоставлять с показанными на карте, где нет искажений или отсутствует один из видов искажений. Величина и характер искажений, который каждый эллипс демонстрирует, следует относить к точке карты, в которой находится центр эллипс.

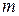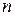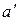Определяя на карте или вычисляя по формулам частные масштабы длин по меридианам и параллелям и угол между ними, легко вычислить параметры эллипса искажений (рисунок 13). Полуоси эллипса искажений и 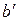(для шара или эллипсоида вращения) находят по формулам:

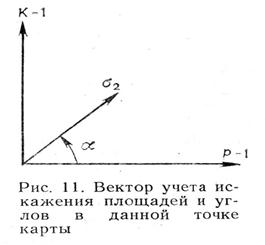
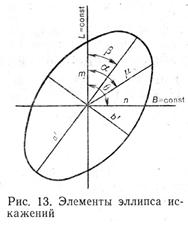
Азимут на карте большой оси эллипса вычисляют по формуле:

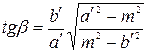
Зная 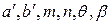нетрудно построит эллипс искажений в заданной точке карты. По этим данным легко найти и другие показатели искажений. Частный масштаб длин 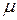по произвольному направлению, определяемому азимута на карте можно найти по формуле:

В пределах карты величины искажений изменяются. В некоторых картографических проекциях имеются центральные точки или линии, в которых искажений (обычно углов) невелики и с удалением от них вначале медленно, а затем ускоренно возрастают. Скорость этого возрастания в разных направлениях может быть различной. Обычно на картах имеются точки или линии, в которых искажения отдельных или всех видов отсутствуют. Это точки и линии нулевых искажений. Места на карте с максимальными искажениями обычно наиболее удалены от линий или точек нулевых искажений. Чтобы обеспечить возможно меньшую величину максимальных искажений, точку или линию нулевых искажений располагают в центре карты. Когда линия замкнута или имеются две линии, их располагают так, чтобы удаления от них к середине и краям карты были примерно одинаковыми. Как изменяются искажения при удалении от точек или линий центральных или нулевых искажений, удобно показывать изоколами.

Изоколы – линии, соединяющие точки с одинаковой величиной того или иного показателя искажений. Изоколы показывают на макетах карты. Обычно в некоторых атласах, а также в учебных пособиях по математической картографии приводятся макеты с изоколами и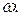

Другой способ показа величин искажений – это составление таблиц с определенным набором показателей искажений.

Выше были рассмотрены локальные показатели. Они характеризуют искажения в точке карты. Иногда при выборе, при искажениях с целью сопоставления разных вариантов проекций пользуются показателями искажений, характеризующими карту в целом. Применяют показатель вариационного типа:

где 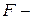площадь изображаемой территории, один из рассматриваемых показателей. Часто интеграл заменяют суммой, для чего изображаемую территорию подразделяют на участки площадью 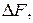для каждого участка находят показатель искажений и вычисляют по формуле:

Дата добавления: 2014-01-20