Примитивный многочлен, его свойства

Разложение многочлена над полем рациональных чисел

Свойство 4

f (x)= f (a ₁)+(x - a ₁) f (a ₁, a ₂)+…+(x - a ₁)…(x - a _k-1) f (a ₁,…. a _k)+ +(x - a ₁)…(x - a _k) f (x, a ₁,…. a _k)

Доказательство. Из определения разности порядка k выразим разность меньшего порядка 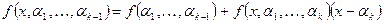. Продолжив этот процесс получим искомую формулу.

Определение 2.2Многочлен над кольцом целых чисел называется примитивным, если наибольший общий делитель его коэффициентов равен 1.

Многочлен с рациональными коэффициентами единственным образом представляется в виде произведения положительного рационального числа и примитивного многочлена. Рациональное число называют содержанием многочлена.

Теорема 2.10 Произведение примитивных многочленов есть примитивный многочлен.

Доказательство проведём методом от противного. Пусть произведение двух примитивных многочленов 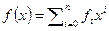и 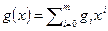есть не примитивный многочлен 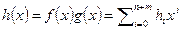. Найдётся простое число p, которое делит все коэффициенты многочлена h(x) без остатка. Пусть 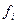-самый младший (с наименьшим номером) коэффициент f(x), не делящийся на p без остатка (такой найдётся в силу примитивности многочлена), а 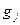- самый младший коэффициент g(x), не делящийся на p без остатка. Коэффициент многочлена h(x) при 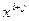вычисляется по формуле 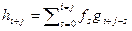. Слагаемое 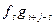делится на p без остатка при s<i, так как левый множитель кратен p, а при s>i, так как правый множитель кратен p. Единственное слагаемое, которое не делится на p, получается при s=i. Следовательно, вся сумма не делится на p, а значит не все коэффициенты h(x) делятся на p, что противоречит сделанному допущению. Тем самым теорема доказана.

Следствие 2.2. Если многочлен с целочисленными коэффициентами приводим над полем рациональных чисел, то он приводим над кольцом целых чисел.

Доказательство. Разложим многочлен над полем рациональных чисел. Каждый множитель представим в виде произведения его содержания и примитивного многочлена. Произведение примитивных многочленов суть примитивный многочлен, поэтому произведение содержаний множителей равно содержанию исходного многочлена. Для завершения доказательства осталось заметить, что содержание исходного многочлена есть целое число.

Таким образом, задача разложения многочлена на неприводимые множители над полем рациональных чисел сводится к аналогичной задаче над кольцом целых чисел.

Дата добавления: 2014-01-20