Критерий Эйзенштейна

Теорема 2.11 (Критерий Эйзенштейна) Пусть f (x) многочлен над кольцом целых чисел. Если существует простое число p, что

I. Все коэффициенты многочлена f (x), кроме старшего, делятся на p

II. Старший коэффициент не делится на p

III. Свободный член не делится на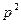

Тогда многочлен f (x) неприводим над полем рациональных чисел.

Доказательство проведём методом от противного. Допустим многочлен h(x) удовлетворяет условиям теоремы и тем не менее представим в виде произведения двух многочленов f(x)g(x). Естественно, все многочлены с целыми коэффициентами. Поскольку 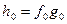, то либо 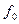делится на p, либо 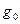делится на p (оба сразу делиться не могут, из-за условия III). Пусть, для определённости 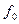делится на p, а 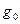не делится на p. Из равенства 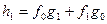, делимост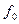и и 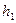на p, и не делимости 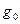на p, выводим делимость 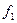на p. Продолжив рассуждения, придём к тому, что все коэффициенты f(x) делятся на p, что противоречит условию I.

Следует отметить, что критерий Эйзенштейна даёт достаточные условия неприводимости многочленов, но не необходимые. Так многочлен 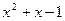является неприводимым над полем рациональных чисел, но не удовлетворяет критерию Эйзенштейна.

Следствие 2.3 Над полем рациональных чисел найдётся неприводимый многочлен степени n, где n любое натуральное число больше 1.

Действительно, многочлен 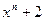, по критерию Эйзенштейна, является неприводимым.

Следствие 2.4 Для простого n многочлен 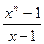неприводим над полем рациональных чисел.

Доказательство. Разложим многочлен по степеням x-1 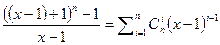. Многочлен 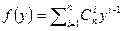удовлетворяет критерию Эйзенштейна, и, значит, является неприводимым. Но тогда неприводим и многочлен .

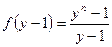Дата добавления: 2014-01-20