Перестановки

Метод Гаусса.

Теорема 3.2 Равносильными преобразованиями, указанными выше (Теорема 3.1) расширенную матрицу можно привести к ступенчатому виду.

Доказательство. Приведём алгоритм приведения матрицы к ступенчатому виду…..

После того как матрица приведена к ступенчатому виду легко построить решение системы линейных уравнений, либо доказать его отсутствие. Если матрица имеет строку, у которой только один ненулевой элемент, расположенный в последнем столбце, то решений нет. В противном случае решение есть и легко строиться.

Определение 4.1. Перестановкой n-го порядка называется взаимно однозначное отображение множества чисел от 1 до n на себя.

Перестановки можно записывать в виде таблицы, где под каждым числом стоит его образ. Например, перестановка 3 порядка 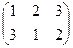переводит 1 в 3, 2 в 1 и 3 в 2.

Лемма 4.1. Число перестановок n-го порядка равно n!.

Доказательство очевидно.

Определение перестановки, как взаимно однозначной функции позволяет перенести понятие суперпозиции функций на перестановки. Пусть перестановка f ставит в соответствие номеру i номер f(i), а перестановка g ставит в соответствие номеру j номер g(j). Рассмотрим функцию f(g(i)). Очевидно, эта функция задает взаимно однозначное отображение множества чисел от 1 до n, и, следовательно, определяет перестановку.

Определение 4.2. Перестановку, определенную функцией f(g(i)) называют суперпозицией или произведением перестановок g и f и обозначают gf.

Для примера найдем суперпозицию перестановок 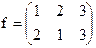и 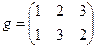. Поскольку f(g(1))=f(1)=2, f(g(2))=f(3)=3, f(g(3))=f(2)=1, то .

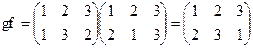Отметим некоторые свойства операции произведения перестановок.

Свойство 4.1 Операция произведения перестановок не коммутативна, то есть в общем случае.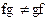

Действительно, 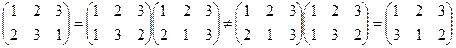Свойство 4.2. Операция умножения перестановок ассоциативна, то есть f(gh)=(fg)h.

Доказательство. В перестановке f(gh) номер i отображается в номер (gh)(f(i))=h(g(f(i))), а в перестановке (fg)h номер i отображается в число h((fg)(i))=h(g(f(i))). В обоих случаях образ совпадает.

Определение 4.3Перестановка 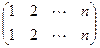называется тождественной, и обозначается e. Перестановка f называется обратной к перестановке g, если fg=e.

Свойство 4.3. Обратная перестановка существует и единственна.

Доказательство очевидным образом следует из определения перестановки как взаимно однозначного соответствия.

Начиная с некоторого номера j, построим последовательность чисел 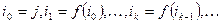. В данной последовательности обязательно наступит повторение, поскольку множество значений перестановки 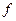конечно. Пусть 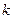- наименьший номер, после которого появляется ранее встречавшееся число в последовательности (т.е. 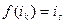и k>s). Если 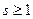, то номер 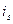является образом двух номеров 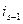и 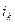, что противоречит определению перестановки как взаимно однозначного соответствия. Следовательно, 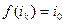, и последовательность 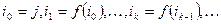, начиная с 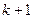члена, начинает повторяться. Не повторяющаяся часть последовательности (т.е. её первые k+1 членов) называется циклом длины k+1.

Циклы называются независимыми, если никакие два цикла не имеют общих номеров.

Кроме табличной записи перестановок существует их запись в виде произведения независимых циклов.

Часто удобно представлять перестановку в виде произведения независимых циклов, а не в табличном виде. В отличие от табличного вида перестановка пишется в строчку. За каждым номером i следует его образ f(i). Номера в цикле разделены тире. Циклы пишутся через запятую. Не пишутся также элементы, которые переходят сами в себя (т.е. циклы длины 1). Например, перестановка 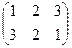запишется как (1-3), а перестановка 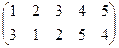запишется как (1-3-2, 4-5)

Дата добавления: 2014-01-20