Конечномерные пространства. Базис. Размерность. Дополнение до базиса. Базис суммы, пересечения

Определение 7.9. Пространство называется конечномерным, если оно является линейной оболочкой конечной системы векторов.

Теорема 7.3. Подпространство конечномерного пространства – конечномерно.

Доказательство. Пусть V – конечномерное пространство, W – его подпространство. По определению, V представляется в виде линейной оболочки конечной системы векторов 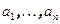. Проведём доказательство теоремы индукцией по n. При n=1 утверждение очевидно, так как любое подпространство, содержащее не нулевой вектор, в этом случае, совпадает с V. Пусть утверждение доказано для n-1. Покажем его справедливость для n. Возьмём не нулевой вектор 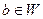и запишем его в виде линейной комбинации 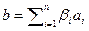. Не нарушая общности можно считать 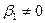(иначе перенумеруем векторы 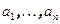). Множество векторов 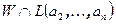образует подпространство в линейной оболочке 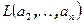и по предположению индукции это подпространство конечномерно. Пусть линейная оболочка векторов 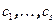совпадает с 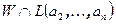. Поскольку векторы 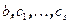принадлежат W, то включение 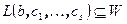очевидно. Пусть 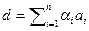- произвольный вектор W. 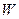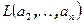Вектор принадлежит подпространству и , а значит, и их пересечению. Представим вектор 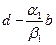в виде линейной комбинации векторов 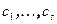и выразим d (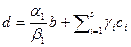). Таким образом, установлено включение , из которого, в силу произвольности выбора d, выводим равенство 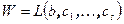, т.е. W - конечномерное подпространство.

Пусть V конечномерное пространство.

Определение 7.10. Минимальная полная система векторов из V называется базисом пространства. Число векторов в базисе называется размерностью пространства.

Размерность пространства V обозначают dimV.

Следствие 7.7 Размерность подпространства не превосходит размерности всего пространства. Если размерность подпространства совпадает с размерностью пространства, то подпространство совпадает с пространством.

Доказательство. Пусть W – подпространство конечномерного пространства V. Обозначим через 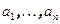базис V. Подпространство W - конечно мерно (Теорема 7.3) и, значит, имеет базис 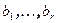. По теореме о замене выполняется неравенство 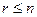. В случае равенства 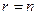из доказательства теоремы о замене вытекает совпадение линейных оболочек .

Определение 7.11. Коэффициенты разложения вектора по базису называются координатами.

Теорема 7.4. Координаты любого вектора существуют и единственны.

Доказательство. Поскольку базис полная система, то любой вектор пространства разложим по базису. Допустим вектор x имеет два различных разложения по базису 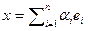и 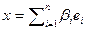. Вычтем одно из другого, получим равенство 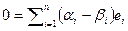. В силу линейной независимости базисных векторов, все коэффициенты при базисных векторах равны нулю, а, значит разложения совпадают.

Координаты вектора в базисе 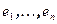обозначим через .

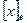Следствие 7.8. Справедливы равенства , , .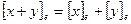

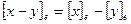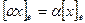Доказательство очевидно.

Теорема 7.5. (дополнение до базиса)

Базис подпространства конечномерного пространства можно дополнить до базиса всего пространства..

Доказательство. Пусть W подпространство V. Обозначим через базис W а через 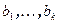- базис V. В системе 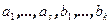удалим векторы, которые линейно выражаются через предыдущие вектора системы. Получившаяся система будет являться базой, а значит образует базис в пространстве V. Кроме того, векторы линейно независимы, и не могут линейно выражаться через предыдущие вектора системы, и значит, они содержатся в базисе. Фактически получается, что система векторов дополнилась некоторыми векторами из базиса V до базиса всего пространства.

Теорема 7.6 (размерность суммы) Пусть V,W – конечномерные подпространства. Тогда .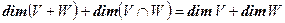

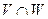Доказательство. Обозначим через базис пространства . Дополним его до базиса пространства V векторами 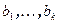(т.е. 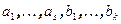- базис V) и до базиса W - векторами (т.е. 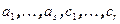- базис W). Легко убедиться, что 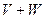совпадает с линейной оболочкой векторов . Далее, система векторов линейно независима. Действительно, если не так, то линейная комбинация этих векторов с не нулевыми коэффициентами равна нулю. Пусть 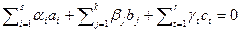. Из равенства 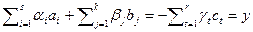выводим, что вектор y принадлежит V и W. Раз вектор y принадлежит пересечению 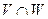, то все 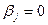(в силу единственности координат), что противоречит линейной независимости системы 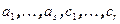. Таким образом, система векторов образует базис 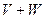. Далее, имеем 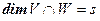, , 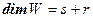и 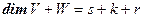. Для завершения доказательства осталось убедиться в справедливости равенства .

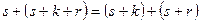Дата добавления: 2014-01-20