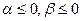Ранги матрицы

Задание прямой и плоскости в пространстве. Деление отрезка. Задачи.

Опишем множество точек, лежащих на прямой l, проходящей через точки A, B. Если 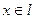, то векторы 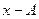и 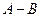коллинеарные, т.е отличаются числовым множителем. Пусть 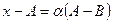. Выразим отсюда x: 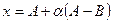. Данное уравнение называется параметрическим уравнением прямой. Вектор A-B принадлежит прямой и называется направляющим вектором прямой.

В зависимости от параметра 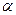получаем различные точки прямой. Если 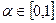, то получим точку X из отрезка 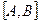, причём 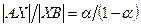. Если 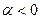, то получаем точку X, что отрезок 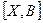содержит точку A, причём 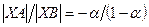. Если 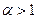, то получаем точку X, что отрезок 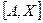содержит точку B, причём .

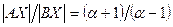Пусть A,B,C три точки не лежащие на одной прямой. Опишем множество точек плоскости 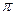, проходящей через эти три точки. Точка x лежит на плоскости тогда и только тогда, когда вектор x-A является линейной комбинацией векторов B-A и C-A. Следовательно, параметрическое уравнение плоскости имеет вид 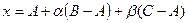. Векторы B-A и C-A называются направляющими векторами плоскости.

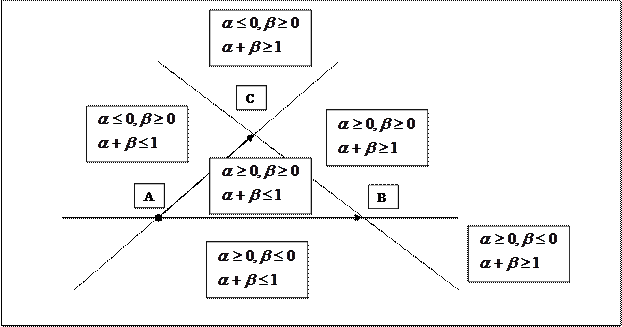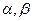В зависимости от значений параметров получаются точки из разных областей. На рисунке приведено разбиение на области и указаны значения параметров.

Пусть система векторов 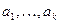- линейно не зависима. Множество точек вида 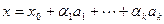называется линейным многообразием.

Для иллюстрации приведённой теории решим следующую задачу:

Доказать, что в произвольном тетраэдре, все отрезки соединяющие вершины с точкой пересечения медиан треугольника, образованного вершинами противоположной грани, пересекаются в одной точке и найти отношение, в котором делит эти отрезки точка пересечения.

В начале решим вспомогательную задачу: выразить точку пересечения медиан треугольника через его вершины. Обозначим вершины треугольника через A,B,C. Векторы AB и AC выберем в качестве базиса. Тогда, точки имеют координаты A=(0,0), B=(1,0), C=(0,1). Обозначим середину отрезка [BC] через F. Точка F имеет координаты (1/2,1/2). Отрезок [AF] делится точкой пересечения медиан O в соотношении 2:1, следовательно, O=(1/3,1/3). Таким образом, 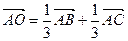. Рассматривая плоскость как линейное многообразие, получаем 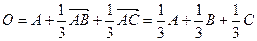. Обозначим через ABCD вершины тетраэдра. В качестве базиса выберем векторы AB, AC, AD. Тогда A=(0,0,0), B=(1,0,0), C=(0,1,0), D=(0,0,1). Точку пересечения медиан треугольника BCD обозначим через F, треугольника ACD – через G. Координаты этих точек равны F=(1/3,1/3,1/3), G=(0,1/3,1/3). Параметрическое уравнение прямой AF имеет вид x=a(1/3,1/3,1/3), а прямой BG x=(1,0,0)+b(-1,1/3,1/3). Точка пересечения H этих прямых находится из системы уравнений a(1/3,1/3,1/3)=(1,0,0)+b(-1,1/3,1/3) и H=(1/4,1/4,1/4) (получается при a=b=3/4). Отрезки AF и BG в точке пересечения делятся в отношении 3:1. Выбирая в качестве B любую вершину тетраэдра (отличную от A) получим, что все отрезки соединяющие вершины с точкой пересечения медиан треугольника, образованного вершинами противоположной грани, пересекаются в одной точке H и делятся в отношении 3:1.

Для матрицы можно дать три определения ранга:

1. Столбцовый ранг - ранг системы столбцов.

2. Строчечный ранг - ранг системы строк.

3. Минорный ранг - Порядок наибольшего (по размеру) отличного от нуля минора.

Теорема 7.11. Все ранги равны.

Доказательство. Для доказательства достаточно показать равенство столбцового и минорного рангов. Действительно, при транспонировании матрицы минорный ранг не меняется, а столбцовый ранг становится строчечным.

Первое доказательство. Воспользуемся критерием линейной независимости (Теорема 7.9).

Второе доказательство. Пусть максимальный по порядку не нулевой минор расположен на пересечении строк с номерами 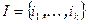и столбцов с номерами из 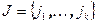. Система линейных уравнений 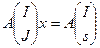, где является крамеровской и, значит, имеет единственное решение, которое равно 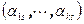. Для 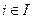выполняется равенство 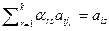, при s=1,…,n. Пусть 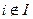, 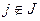. Рассмотрим минор 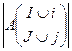. Вычтем из последнего столбца остальные столбцы с коэффициентами 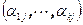и разложим по последнему столбцу. В результате получим 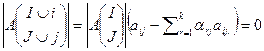(все миноры порядка больше k равны 0). Поскольку 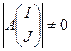, то равенство выполняется при . 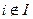Таким образом, все столбцы линейно выражаются через столбцы с номерами из множества 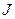. Система уравнений 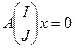имеет единственное нулевое решение, следовательно, столбцы матрицы A с номерами из J образуют базу. Ранг системы столбцов совпадает с порядком максимального не нулевого минора, что и требовалось доказать.

Следствие 7.11. Ранг произведения матриц не превосходит ранга сомножителей.

Доказательство. Пусть C=AB. По определению произведения матриц, строки матрицы C являются линейными комбинациями строк матрицы B и, значит, 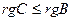. Аналогично, столбцы матрицы C – линейные комбинации столбцов матрицы A, и .

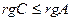Дата добавления: 2014-01-20