Изобарный процесс

Условие, определяющее этот процесс: р = const или dp = 0.

В pυ -координатах изображается горизонтальными линями на рис. 15.3.

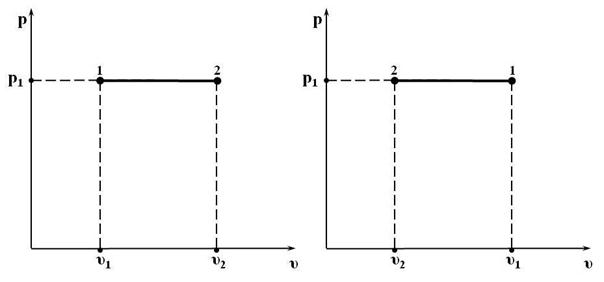
Рис. 15.3. Изобарный процесс 1 – 2 в р υ -координатах:

а) с увеличением удельного объёма (расширение); б) с уменьшением удельного объёма (сжатие)

Соотношение между параметрами состояния в ходе изобарного процесса определяется из уравнения состояния идеального газа. Запишем его для точек 1 и 2 – начала и конца изобарного процесса:

. (15.1)

Разделив левые и правые части (15.1) друг на друга получаем:

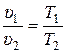. (15.2)

Равенство (15.2) показывает, что в изобарном процессе отношение удельных объёмов равно отношению температур.

Исходная система уравнений (15.6) с дополнительным условием для изобарного процесса имеет вид:

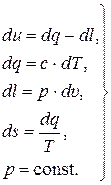(15.3)

Благодаря последнему в (15.3) условию неизвестная в общем случае истинная удельная теплоёмкость с становится известной (из справочника) удельной теплоёмкостью с_р при постоянном давлении. В результате в системе (15.3) число неизвестных функций становится равным числу независимых уравнений, и система становится однозначно разрешаемой.

В результате интегрирования второго уравнения в (15.3) получаем:

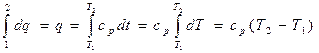. (15.4)

В результате интегрирования третьего уравнения получаем:

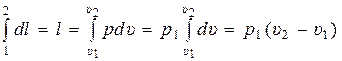. (15.5)

В результате интегрирования первого уравнения получаем:

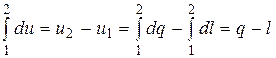. (15.6)

В результате интегрирования четвёртого уравнения получаем:

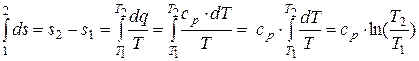. (15.7)

Выводы:

1) Из (15.6) с учётом (15.5) и того, что р ₁ = р ₂, следует:

q = u ₂ – u ₁ + l = u ₂ – u ₁ + p ₁ · (υ ₂ – υ ₁) = u ₂ – u ₁ + p ₂ υ ₂ – p ₁ υ ₁ =

= (u ₂ + p ₂ υ ₂) – (u ₁ + p ₁ υ ₁) = i ₂ – i ₁, (15.8)

где i ₁ и i ₂ – удельные энтальпии газа в начале и конце изобарного процесса, Дж/кг.

Формула (15.8) показывает, что теплота в изобарном процессе расходуется на изменение удельной энтальпии системы. (В то время как в изохорном – на изменение удельной внутренней энергии).

С учётом (15.4) вместо (15.8) можем записать:

i ₂ – i ₁ = с_р (Т ₂ – Т ₁). (15.9)

При известной с_р выражение (15.9) позволяет построить таблицы для удельной энтальпии, как функции состояния.

2) Используя уравнение идеального газа из (15.5) получаем:

l = р ₁ · (υ ₂ – υ ₁) = p ₂ υ ₂ – p ₁ υ ₁ = RT ₂ – RT ₁ = R · (T ₂ – T ₁). (15.10)

Рассмотрим далее случай, когда (Т ₂ – Т ₁) = 1, К. Тогда из (15.10) будем иметь:

l = R · 1, Дж/кг. (15.11)

Равенство (15.11) показывает, что газовая постоянная численно равна работе одного килограмма газа в изобарном процессе при увеличении его температуры на один градус.

3) Из (15.7) следует, что изобарный процесс в T s -координатах является логарифмической кривой, рис. 15.4.

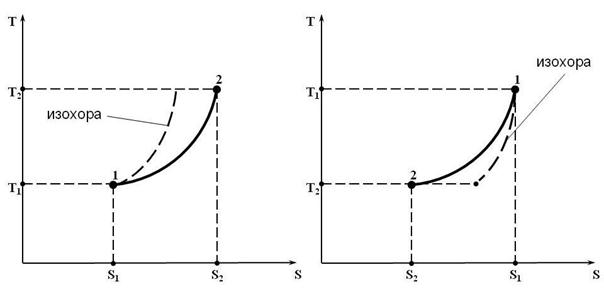
Рис. 15.4. Изобарный процесс 1 – 2 в T s -координатах:

а) с подводом теплоты; б) с отводом теплоты

На рис. 15.4 для качественного сравнения в том же диапазоне температур пунктирной линией изображена изохора, которая идёт круче изобары.

Дата добавления: 2014-01-20