Химический состав газовой смеси

Химический состав газовой смеси может задаваться тремя различными способами.

Рассмотрим газовую смесь, состоящую из n компонентов. Смесь занимает объём V _см, м³, имеет массу М _см, кг, давление р _см, Па и температуру Т _см, К. Также число молей смеси равно N _см, моль. При этом масса одного i -го компонента m_i, кг, а число молей этого компонента ν_i, моль.

Очевидно, что:

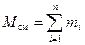, (4)

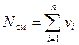. (5)

Используя для рассматриваемой смеси закон Дальтона (2) и Амага (3) можно записать:

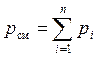, (6)

, (7)

где р_i – парциальное давление i -го компонента, Па; V_i – приведённый объём i -го компонента, м³.

Однозначно химический состав газовой смеси может быть задан либо массовыми, либо мольными, либо объёмными долями её компонентов:

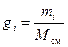, (8)

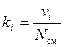, (9)

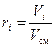, (10)

где g_i, k_i и r_i – массовая, мольная и объёмная доли i -го компонента смеси соответственно (безразмерные величины).

Очевидно, что:

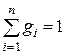, , . (11)

Часто на практике химический состав смеси задаётся не долями i -го компонента, а его процентами.

Например, в теплотехнике приближённо принимается, что сухой воздух состоит из 79 объёмных процентов азота и 21 объёмного процента кислорода.

Процент i-го компонента в смеси вычисляется путём умножения его доли на 100.

Для примера с сухим воздухом будем иметь:

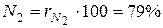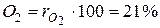, . (12)

где и 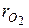– объёмные доли азота и кислорода в сухом воздухе; N₂ и О₂ – обозначение объёмных процентов азота и кислорода соответственно, % (об.).

Примечание:

1) Мольные доли идеальной смеси численно равны объёмным долям: k_i = r_i. Докажем это.

Пользуясь определением объёмной доли (10) и законом Амага можем записать:

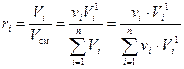, (13)

где V_i – приведённый объём i-го компонента, м³; ν_i – число молей i-го компонента, моль; – объём одного моля i-го компонента при давлении смеси р _см и температуре смеси Т _см, м³/моль.

Из закона Авогадро (см. п. 2.3) данного приложения следует, что при одинаковых температуре и давлении один моль любого газа (компонента смеси) занимает один и тот же объём, в частности, при Т _см и р _см это будет некоторый объём V ¹, м³.

Сказанное позволяет записать равенство:

. (14)

Подставляя (14) в (13) получаем требуемое:

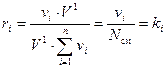. (15)

2) Объёмные доли компонентов газовой смеси можно рассчитать, зная их парциальные давления. Покажем это.

Рассмотрим i-ый компонент идеальной газовой смеси в двух различных состояниях: когда он находится при своём парциальном давлении р_i; когда он занимает свой приведённый объём V_i.

Уравнение состояния идеального газа справедливо для любых его состояний, в частности, и для двух, названных выше.

В соответствии с этим, и учитывая определение удельного объёма, можем записать:

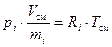, (16)

и

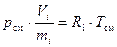, (17)

где R_i – газовая постоянная i-го компонента смеси, Дж/(кг · К).

После деления обоих частей (16) и (17) друг на друга получаем требуемое:

. (18)

Из (18) видно, что парциальные давления компонентов смеси можно рассчитать по её химическому составу, при известном общем давлении смеси р _см:

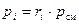. (19)

Дата добавления: 2014-01-20