Свободные колебания в LC-контуре. Свободные затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ

Электромагнитными колебаниями называются переодические изменения во времени значений силы тока и напряжения в электрической цепи, а также обусловленные этим взаимосвязанные колебания электрического и магнитного полей, которые описывают соответственно векторы Е и Н. Наиболее распространенной электрической цепью, в которой возникают такие колебания, является электрический колебательный контур, содержащий последовательно соединенные конденсатор емкостью С, катушку индуктивностью L и резистор сопротивлением R, рис.1.

- С+ I=dq/dt

- +

φ₂ φ₁> φ₂

R L

K E_c =- LdI/dt

I

Рис.1.

Если сопротивление R мало (R→0) электрический контур является идеальным ( LC – контур). При R≠0 часть электрической энергии будет расходоваться на нагревание проводников и будет наблюдаться затухание колебательных процессов.

Свободные колебания в LC-контуре. Колебания электрического тока в контуре можно вызвать, либо сообщив обкладкам конденсатора некоторый начальный заряд, либо возбудив в индуктивности ток. Воспользуемся первым способом. При разомкнутом ключе зарядим конденсатор. Между обкладками конденсатора возникнет электрическое поле, энергия которого W_C = q²/2C. После замыкания ключа К емкость начнет разряжаться и в контуре потечет электрический ток. В результате энергия электрического поля будет уменьшаться, зато возникнет и начнет увеличиваться энергия магнитного поля, обусловленного током, текущим через индуктивность. Энергия магнитного поля W_L=LI²/2. Если R = 0, то в момент когда напряжение на конденсаторе, заряд, а следовательно и энергия W_C обращаются в нуль, энергия магнитного поля, а следовательно и ток достигают наибольшего значения (начиная с этого момента ток течет за счет э.д.с. самоиндукции). В дальнейшем ток уменьшается и, когда заряды на обкладках конденсатора достигнут первоначального значения q (но противоположных знаков), сила тока станет равной нулю. После этого те же процессы начнут протекать в обратном направлении, контур вернется в исходное состояние и весь цикл повторится снова и снова. Колебания электрического тока (заряда, напряжения) сопровождаются взаимными превращениями энергий электрического и магнитного полей.

Будем обходить контур против часовой стрелки. При возрастании значения заряда на положительно заряженной обкладке конденсатора сила тока

I = dq/dt. (1)

Для расчета электрической цепи запишем закон Ома

IR = φ₁ – φ₂ + E_C. (2)

Поскольку разность потенциалов между обкладками φ₁ – φ₂ =q/C, а э.д.с. самоиндукции E_c =- LdI/dt, то равенство (2) можно переписать в виде дифференциального уравнения второго порядка по отношению к заряду q=q(t):

Ld²q/dt² +Rdq/dt + q/C = 0. (3)

Если учесть, что R = 0, ииспользовать стандартные обозначения для собственной частоты ω₀ гармонических колебаний:

ω₀ = 1/√LC, (4)

то уравнение (3) примет вид

d²q/dt² + ω₀²q = 0. (3а)

Решением уравнения (3а) является функция

q = q_mcos(ω₀t + α). (5)

Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой ω₀ = 1/√LC, которая называется собственной частотой контура, она соответствует собственной частоте гармонического осциллятора.

Из (4) получаем выражение для периода колебаний (формула Томсона):

T = 2π√(LC). (6)

Используя известную формулу q = UC и (5), запишем выражение для напряжения на конденсаторе:

U = (1/C)q_mcos(ω₀t + α) = U_m cos(ω₀t + α). (7)

Продифференцировав функцию (5) по времени, получим выражение для силы тока в контуре:

I = - ω₀q_m sin(ω₀t + α) = I_m cos(ω₀t + α + π/2). (8)

Из (8) видно, что сила тока опережает по фазе напряжение на конденсаторе на π/2. Сопоставление формул (5), (7) и (8) показывает, что в момент, когда ток достигает наибольшего значения, заряд и напряжение обращаются в нуль, и наоборот, как мы уже это установили ранее, основываясь на энергетических соображениях.

U_m=q_m/C, I_m = ω₀q_m, U_m = I_m√(L/C).

Свободные затухающие колебания. Поскольку всякий реальный контур обладает активным сопротивлением R≠0, то введя обозначение β=R/(2L) уравнение (3) можно переписать следующим образом

d²q/dt² + 2βdq/dt + ω₀²q = 0. (9)

(9) – дифференциальное уравнение свободных затухающих колебаний.

При условии, что β<ω₀ решение уравнения (9) для заряда q имеет вид затухающих колебаний:

q = q_m e^-βt cos(ωt + α), (10)

где ω = √(ω₀² – β²) - частота затухающих колебаний.

После подстановки в последнее выражение значений для ω₀ и β, получим

ω = √(1/LC – R²/4L²). (11)

Т.О., ω<ω₀^. При R = 0 выражение (11) переходит в (4).

Колебания заряда на обкладках конденсатора происходят с периодом

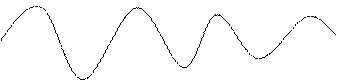
Т = 2π/ω и убывающей амплитудой q_m (t) = q_mexp(-Rt/2L), рис.2.

q

t

Рис.2.

Характерное время затухания электрических колебаний в контуре определяется временем релаксации

τ = 1/β = 2L/R,

т.е. индуктивность является мерой инертности для электрических колебаний заряда, а значит, и силы тока в контуре.

Напряжение на конденсаторе пропорционально заряду q, поэтому оно изменяется синхронно с зарядом q, а сила тока

I = dq/dt = q_m e^-βt [-βcos(ωt + α) – ωsin(ωt + α)].

Это выражение можно преобразовать к виду

I = I_me^-βtcos(ωt + α +Δ) (12)

Из (12) видно, что сила тока также затухает со временем, однако колебания тока происходят с некоторым опережением по фазе (Δ) относительно колебания заряда (напряжения) на конденсаторе.

Затухание колебаний принято характеризовать логарифмическим декрементом затухания

λ = ln a (t)/ a (t+T) = βT, (13)

где a (t) – амплитуда соответствующей величины (q,U или I). Вспомним, что λ = 1/N_e, где N_e- число колебаний, совершаемых за время, в течение которого амплитуда уменьшается в е раз.

Подставив в (13) значение для β=R/2L и Т=2π/ω, получим

λ = (R/2L)(2π/ω) = πR/Lω, (14)

т.е. логарифмический декремент затухания определяется параметрами контура L,C и R и является характеристикой контура.

Если затухание невелико (β<<ω₀), то в (14) можно считать ω ≈ ω₀ =1/√LC. Тогда

λ ≈ (πR/L)√(LC) = πR√(C/L).

Это выражение по форме аналогично закону Ома (U = I/R), поэтому величину √(C/L), которая имеет размерность электрического сопротивления, называют волновым сопротивлением.

Колебательный контур часто характеризуют его добротностью Q, которая определяется как величина, обратно пропорциональная логарифмическому декременту затухания

Q = π/λ = πN_e. (15)

Видно, что добротность контура тем больше, чем большее число колебаний он успевает совершить, прежде чем амплитуда колебаний уменьшиться в е раз. В случае слабого затухания

Q = (1/R)√(L/C).

Отметим, что при β² ≥ ω₀² вместо колебаний в контуре происходит апериодический разряд конденсатора. Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим. Значение критического сопротивления R_k определяется условием R_k²/4L² = 1/LC, откуда

R_k = 2√(L/C).

Дата добавления: 2014-01-20