Принцип Гюйгенса - Френеля. Зоны Френеля. Дифракция Френеля на круглом экране и круглом отверстии

ДИФРАКЦИЯ СВЕТА

Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Огибание препятствий звуковыми волнами (т.е. дифракция звуковых волн) наблюдается постоянно в обыденной жизни. Например, звук хорошо слышен за углом дома, т.е. звуковая волна его огибает. Для наблюдения дифракции световых волн необходимо создание спец. условий. Это обусловлено малостью длин световых волн. В пределе при l®0 законы волновой оптики переходят в законы геометрической оптики. Следовательно, отклонения от законов геометрической оптики при прочих равных условиях оказываются тем меньше, чем меньше длина волны. Между интерференцией и дифракцией нет существ, различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. По историческим причинам перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть интерференцией волн, а вследствие суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, принято называть дифракцией.

Наблюдение дифракции осуществляется обычно по следующей схеме. На пути св. волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности св. волны. За преградой располагается экран, на котором возникает дифракционная картина.

Различают два вида дифракции. Если источник света S и точка наблюдения М расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку М образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера. В противном случае говорят о дифракции Френеля.

Рис.

Проникновение световых волн в область геометрической тени можно объяснить с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Однако этот принцип не дает сведений об амплитуде (интенсивности) волн, распространяющихся в различных направлениях. Френель дополнил пр. Гюйгенса представлением об интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. Развитый т.о. принцип Гюйгенса получил название принципа Гюйгенса - Френеля: все источники вторичных волн, расположенные на поверхности фронта волны, когерентны между собой; световая волна в любой точке пространства является результатом интерференции волн, излучаемых вторичными источниками и достигших этой точки. Френель исключил возможность возникновения обратных вторичных волн. Поскольку точек фронта, являющихся когерентными источниками новых волн, бесчисленное множество, то расчет интерференции, в принципе, сводится к довольно громоздкому интегрированию. Для упрощения решения этого вопроса Френелем был предложен метод разделения фронта волны на зоны, так что волны от соседних зон приходят в точку наблюдения в противоположной фазе и ослабляют друг друга. С этим методом зон Френеля ознакомимся при анализе важнейшего вопроса: как волновая теория объясняет практическую прямолинейность распространения света и каковы границы применимости законов геометрической оптики, основанных на этой прямолинейности.

Пусть S - точечный источник монохроматического света в однородной среде. По принципу Гюйгенса от него распространяется во все стороны сферическая волна. В некоторый момент времени фронт этой волны занимает положение Ф, рис.1. Рассмотрим произвольную точку М перед фронтом и соединим её прямой линией с источником S.

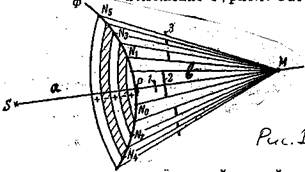
Если бы свет распространялся прямолинейно вдоль луча SРМ, то достаточно было бы поставить на его пути сколь угодно малый экран 1, чтобы в точке М была полная темнота. Благодаря волновой природе света в точку наблюдения М приходят волны не только от точки Р, но и от всех остальных точек фронта Ф, правда в различных фазах.

Для расчета результатов интерференции Френель предложил провести ряд сфер с центрами в точке М и радиусами, соответственно равными

МN₁ = МP +l/2,

MN₂ = МN₁ +l/2 = МP + 2l/2,

MN₃ = МN₂ +l/2 = МP + 3l/2, и т.д. (1)

Тем самым фронт волны Ф разобьется на ряд кольцевых зон, заштрихованных на рис.1 через одну. Волны, приходящие в М от точек каждой последующей зоны, сдвинуты по отношению к волнам, приходящим от соответствующих точек предыдущей зоны, на λ/2, т.е. находятся в противоположных фазах, и их амплитуды при интерференции вычитаются. Из геометрического рассмотрения можно получить выражение для радиуса внешней границы m - ной зоны: r_m=√abmλ/(a + b), если а = b = 1 м и λ = 0,5 мкм, то r₁ = 0,5 нм.

Занумеруем величины суммарных амплитуд волн, приходящих в точку М от каждой последующей зоны:

А₀, А₁, А₂, а₃, А₄, А₅, А₆,....

Благодаря различию в расстояниях зон до точки наблюдения и в углах, под которыми видны эти площадки из М, величины этих амплитуд монотонно убывают:

А₀ > А₁> А₂> а₃> А₄> А₅> А₆,....

В качестве допустимого приближения можно принять, что амплитуда колебания от некоторой k - той зоны Френеля А_k равна среднему арифметическому от амплитуд примыкающих к ней зон:

А_k = (А_k+1 + А_k-1)/2. (2)

Полная амлитуда волны, приходящей в точку М, равна сумме амплитуд, создаваемых каждой отдельной зоной. При этом амплитуды от всех четных зон надо считать с одинаковым знаком (например, положительными), а амплитуда волн от всех нечетных зон (приходящих в точку М) - с обратным знаком. Т.о.,

А = А₀-А₁ + А₂ –А₃,+ А₄- А₅ +.... (3)

Используя (2), можно это выражение представить в виде

А = А₀/2 + (А₀/2 – А₁ +А₂/2) + (А₂/2 -Аз + А₄ /2) +...» А₀/2, (4)

так как оставшаяся часть от амплитуды последней зоны ±А _k /2 практически ничтожно мала.

Т.о., суммарная амплитуда от воздействия всего фронта Ф в точке наблюдения М равна А = А₀/2, т.е. эквивалентна половине воздействия нулевой зоны Френеля.

Не следует при этом думать, что в М приходит свет только от всех точек половины нулевой зоны Френеля, остальные же участки фронта Ф, интерферируя, гасят др. др.

Дата добавления: 2014-01-20