Вероятностный смысл математического ожидания

Пусть произведено n испытаний, в которых случайная величина X приняла m ₁ раз значение х ₁, m ₂ раз значение х ₂,..., m_k paз значение x_k, причем m ₁ + m ₂ + … + m_k = n. Тогда сумма всех значений, принятых X, равна

х ₁ m ₁ + х ₂ m ₂ + … + x_km_k.

Найдем среднее арифметическое 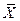всех значений, принятых случайной величиной, для чего разделим найденную сумму на общее число испытаний:

,

или

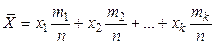. (6.2)

Заметив, что отношение m ₁/ n – относительная частота W ₁ значения х ₁, m ₂/ n – относительная частота W ₂ значения х ₂ и т.д., запишем соотношение (6.2) так:

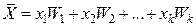. (6.3)

Допустим, что число испытаний достаточно велико. Тогда относительная частота приближенно равна вероятности появления события, что будет будет доказано в дальнейшем:

W ₁» p ₁, W ₂» p ₂, …, W _k» p _k.

Заменив в соотношении (6.3) относительные частоты соответствующими вероятностями, получим

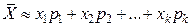
Правая часть этого приближенного равенства есть М (X). Итак,

.

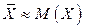Вероятностный смысл полученного результата таков: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

Замечание 1. Легко сообразить, что математическое ожидание больше наименьшего и меньше наибольшего возможных значений. Другими словами, на числовой оси возможные значения расположены слева и справа от математического ожидания. В этом смысле математическое ожидание характеризует расположение распределения и поэтому его часто называют центром распределения.

Этот термин заимствован из механики: если массы р ₁, р ₂,..., р_n расположены в точках с абсциссами x ₁, x ₂,..., х_n, причем 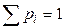, то абсцисса центра тяжести

.

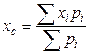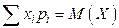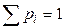Учитывая, что и , получим М (Х) = х_с.

Итак, математическое ожидание есть абсцисса центра тяжести системы материальных точек, абсциссы которых равны возможным значениям случайной величины, а массы – их вероятностям.

Замечание 2. Происхождение термина «математическое ожидание» связано с начальным периодом возникновения теории вероятностей (XVI – XVII вв.), когда область ее применения ограничивалась азартными играми. Игрока интересовало среднее значение ожидаемого выигрыша, или, иными словами, математическое ожидание выигрыша.

Дата добавления: 2014-01-20