Числовые характеристики непрерывных случайных величин

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Распространим определения числовых характеристик дискретных величин на величины непрерывные. Пусть непрерывная случайная величина X задана плотностью распределения f (х). Допустим, что все возможные значения X принадлежат отрезку [ а, b ]. Разобьем этот отрезок на n частичных отрезков длиной D x ₁, D x ₂,..., D x_n и выберем в каждом из них произвольную точку х_i (i = 1, 2,..., n). Необходимо определить математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений х_i на вероятности попадания их в интервал D х_i (напомним, что произведение f (х)D x приближенно равно вероятности попадания X в интервал D x):

.

Перейдя к пределу при стремлении к нулю длины наибольшего из частичных отрезков, получим определенный интеграл .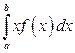

Определение. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [ а, b ], называют определенный интеграл

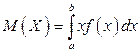. (11.1)

Если возможные значения принадлежат всей оси Ох, то

.

Предполагается, что несобственный интеграл сходится абсолютно, т.е. существует интеграл . Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к – ¥, а верхнего – к +¥.

По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины.

Определение. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения X принадлежат отрезку [ а, b ], то

;

если возможные значения принадлежат всей оси х, то

.

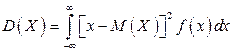Определение. Среднее кеадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством

.

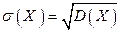Замечание 1. Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.

Замечание 2. Легко получить для вычисления дисперсии более удобные формулы:

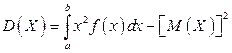, (11.2)

.

Пример 1. Найти математическое ожидание и дисперсию случайной величины X, заданной функцией распределения

Решение. Найдем плотность распределения:

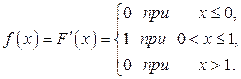
Найдем математическое ожидание по формуле (11.1):

.

Найдем дисперсию по формуле (11.2):

.

Пример 2. Найти математическое ожидание н дисперсию непрерывной случайной величины X, распределенной равномерно в интервале (а, b).

Решение. Найдем математическое ожидание X по формуле (11.1), учитывая, что плотность равномерного распределения f (x) = 1/(b – a)

.

Выполнив элементарные преобразования, получим

.

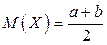Найдем дисперсию X по формуле (11.2):

.

Выполнив элементарные преобразования, получим

.

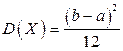Замечание 3. Математическое ожидание и дисперсия случайной величины R, распределенной равномерно в интервале (0, 1), т.е. если а = 0, b = 1, как следует из примера 2, соответственно равны M (R) =1/2, D (R) = 1/12. Этот же результат был получен в примере 1 по заданной функции распределения случайной величины R.

Определение. Модой д.с.в. Х называется ее значение, принимаемое с наибольшей вероятностью по сравнению с двумя соседними значениями, обозначается через М ₀ Х. Для н.с.в. М ₀ Х – точка максимума (локального) плотности f (x).

Если мода единственна, то распределение с.в. называют унимодальным, в противном случае – полимодальным (рис. 11.1).

Определение. Медианой М_еХ н.с.в. Х называется такое ее значение х_р, для которого

, (11.3)

то есть одинаково вероятно, окажется ли с.в. Х меньше х_р или больше х_р (рис. 11.1).

С помощью функции распределения F (x) равенство (11.3) можно записать в виде F (М_еХ) = 1 – F (М_еХ). Отсюда F (М_еХ) = 1/2.

Для д.с.в. медиана обычно не определяется.

Рис. 11.1

Математическое ожидание и дисперсия являются частными случаями следующих более общих понятий – моментов с.в.

Определение. Начальным моментом порядка k с.в. Х называется м.о. k -й степени этой величины, обозначается через v_k.

Таким образом, по определению v_k = M [ X^k ]. Для д.с.в. начальный момент выражается суммой

,

а для н.с.в. – интегралом

.

В частности, v ₁ = M [ X ], то есть начальный момент первого порядка есть м.о.

Определение. Центральным моментом порядка k с.в. Х называется м.о. величины (X – M [ X ]) ^k, обозначается через m _k.

Таким образом, по определению m _k = М (X – M [ X ]) ^k. В частности, m₂ = D [ X ], то есть центральный момент второго порядка есть дисперсия, m₁ = М (X – M [ X ]) = 0.

Для д.с.в. центральный момент равен

,

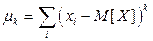а для н.с.в.:

.

Среди моментов высших порядков для н.с.в. особое значение имеют центральные моменты 3-го и 4-го порядков, называемые соответственно коэффициентами асимметрии и эксцесса.

Определение. Коэффициентом асимметрии («скошенности») А с.в. Х называется величина

.

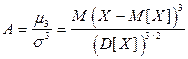Если А > 0, то кривая распределения более полога справа от М ₀ Х (рис. 11.2). Если А < 0, кривая распределения более полога слева от М ₀ Х (рис. 11.3).

Рис. 11.2 Рис. 11.3

Определение. Коэффициентом эксцесса («островершинности») Е с.в. Х называется величина

.

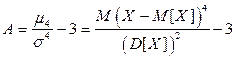Величина Е характеризует островершинность или плосковершинность распределения. Для нормального закона распределения А = 0, Е = 0; остальные распределения сравниваются с нормальным: если E > 0 – более островершинные, а распределения «плосковершинные» имеют E < 0 (рис. 11.4).

Рис. 11.4

Кроме рассмотренных выше числовых характеристик с.в., в приложениях используются так называемые квантили.

Определение. Квантилью уровня р с.в. Х называется решение уравнения

,

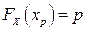где р – некоторое число, 0< p < 1.

Квантили х _0,25, х _0,5, х _0,75 имеют свои названия: нижняя квантиль, медиана (М_еХ = х _0,5), верхняя квантиль соответственно. Они делят числовую прямую на 4 части, вероятности попадания в которые равны 0,25 (рис. 11.5).

Рис. 11.5

Дата добавления: 2014-01-20