Высказывания и операции над ними. Формулы

Тема 1. АЛГЕБРА ВЫСКАЗЫВАНИЙ

Введение

Интернет-ресурсы

1. http://web.redline.ru/education/valdorfru.html - Сервер по Вальдорфской педагогике.

2. http://biblio.narod.ru/gyrnal/vek/sod_vse_tabl.htm - Век образования.Cайт журнала “Education+”.

3. http://biblio.narod.ru/gyrnal/montes/mont_sod.htm - О Монтессори-педагогике. Cайт журнала “Education+”

4. http://hist-ped.chat.ru - История педагогики: педагогические концепции и воззрения российских и зарубежных деятелей педагогики и народного образования

5. http://antonmakarenko.narod.ru - Международная ассоциация Макаренко А.С.

6. http://gymn-edu.narod.ru/index.html - Гимназическое образование

7. http://pedagogics.narod.ru Педагогика российского зарубежья. Сайт Российского гуманитарного научного фонда.

8. http://museum.edu.ru/ Коллекция: история образования. Раздел Российского общеобразовательного портала.

9. http://www.gala-d.ru/ История педагогики.

10. http://www.lib.tsu.ru/win/produkzija/gimnazii/1_1istor.html Традиции и инновационные процессы в практике школьного дела России. Краткий библиографический справочник.

11. http://www.pedobzor.ru/ Педагогика и образование прошлых лет. Электронная библиотека.

Классическая логика исследует процессы умозаключений и позволяет из истинности одних суждений делать выводы об истинности или ложности других, независимо от их конкретного содержания. Использование в логике математических методов (алгебраизация логики и построение логических исчислений) дало начало развитию новой области математики, называемой «Математической логикой». Основная задача математической логики – формализация знаний и рассуждений.

Основные понятия математической логики лежат в основе таких ее приложений, как базы данных, экспертные системы, системы логического программирования.

Существуют два подхода к рассмотрению вопросов, которыми занимается математическая логика:

- семантическая (смысловая) теория, в основе которой лежит понятие алгебры;

- формально-аксиоматическая (синтаксическая) теория, базирующаяся на понятии логического исчисления.

В данном курсе рассматриваются оба этих подхода. Начнём с алгебры высказываний, которая затем обобщается алгеброй предикатов. Затем обе они послужат пониманию построения логических исчислений и их частных случаев: исчисления высказываний и исчисления предикатов.

Высказыванием называется всякое утверждение, о котором можно вполне определенно и объективно сказать истинно оно или ложно.

Например, утверждение "2 > 0" является высказыванием и оно истинно, а утверждение "2 < 0" – ложно, утверждение "x² + y² = z²" высказыванием не является, так как оно может быть, как истинным, так и ложным при различных значениях переменных x, y, z. Высказывание полностью определяется своим истинностным значением. Условимся, значение истинности высказывания обозначать 1 (или И), если высказывание истинно, и 0 (или Л), если ложно.

Различают высказывания простые и сложные. Высказывание называется простым, если никакая его часть не является высказыванием. Простые высказывания будем обозначать начальными заглавными буквами латинского алфавита A, B, C или A₁, A₂,.... Сложные высказывания характеризуются тем, что они образованы из нескольких простых высказываний с помощью логических операций, т.е. являются формулами алгебры высказываний.

Напомним, что в дискретной математике алгебраической структурой или алгеброй называется структура, образованная некоторым множеством вместе с введенными на нём операциями. Определим алгебру высказываний.

Обозначим через B = {0, 1} – множество высказываний. Определим операции на множестве B.

Отрицанием высказывания A называется высказывание, которое принимает значение истина, если A ложно, и наоборот. Отрицание обозначается 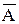(ØА) и является унарной операцией.

Пусть А и В – некоторые высказывания, введем бинарные операции над ними.

Конъюнкцией высказываний A и B называется высказывание, которое принимает значение истина тогда и только тогда, когда истинны оба высказывания A и B. Обозначается конъюнкция – A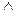B (А&В).

Дизъюнкцией высказываний A и B называется высказывание, которое принимает значение истина, если истинно хотя бы одно из высказываний A или B. Обозначается дизъюнкция – A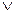B.

Импликацией высказываний A и B называется высказывание, которое принимает значение ложь тогда и только тогда, когда A истинно, а B ложно. Обозначается А®В.

Эквиваленцией высказываний A и B называется высказывание, которое принимает значение истина тогда и только тогда, когда высказывания A и B имеют одинаковые значения. Обозначение операции – А~В (АºВ).

Логические операции определяются, также, с помощью таблиц, называемых таблицами истинности. Приведем сводную таблицу истинности для всех введенных логических операций.

A	B	ØA	AÙB	AÚB	A®B	A~B

Пропозициональной (высказывательной) переменной называется переменная, значениями которой являются простые высказывания. Обозначим высказывательные переменные через X₁, X₂,..., X_n.

Понятие формулы алгебры высказываний вводится по индукции. Формулами алгебры высказываний являются:

1) логические константы 0 и 1;

2) пропозициональные переменные;

3) если А и В – формулы, то каждое из выражений Ø(А), (А) Ù (В), (А) Ú (В), (А) ® (В), (А) ~ (В) есть формула;

4) других формул, кроме построенных по пп. 1) – 3), нет.

Для формулы построенной по п. 3 формулы A и B называются подформулами. Число скобок в формуле можно сократить.

Порядок выполнения операций в формуле определяется их приоритетом. Список логических операций в порядке убывания приоритета: 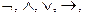~. Изменение порядка выполнения операций, как и в алгебраических операциях, производится с помощью круглых скобок.

Пусть U – формула над высказывательными переменными X₁, X₂,..., X_n, обозначается U (X₁, X₂,..., X_n). Набор конкретных значений высказывательных переменных X₁, X₂,..., X_n называется интерпретацией формулы U и обозначается I (U).

Формула называется выполнимой, если существует такой набор значений переменных, при которых эта формула принимает значение 1 – истина (существует интерпритация I (U), на которой формула истинна).

Формула называется опровержимой, если существует такой набор значений переменных, при которых эта формула принимает значение 0 – ложь (существует интерпритация I (U), на которой формула ложна).

Формула называется тождественно истинной (ТИ-формулой) или тавтологией, если эта формула принимает значение 1 при всех наборах значений переменных (формула истинна на всех интерпретациях).

Формула называется тождественно ложной (ТЛ-формулой) или противоречием, если эта формула принимает значение 0 при всех наборах значений переменных (формула ложна на всех интерпретациях).

Формулы А и В называются эквивалентными (обозначается А º В), если при любых значениях высказывательных переменных значение формулы А совпадает со значением формулы В.

Дата добавления: 2014-01-20