Векторно-растровое преобразование

Векторно-растровое преобразование можно использовать для генерализации изображения. При этом существенное значение имеет разрешающая способность создаваемой (электронной) карты. Преобразование типа вектор-растр — более простая задача. Оно осуществляется при выводе векторных данных на устройства печати, при визуализации графики на растровых видемониторах, построении электронных карт или карт-подложек.

К этой же группе операций относят сжатие или развертку растровых данных, основанных на алгоритмах кодирования и компрессии, разбиения на слои, фрагментации или дефрагментации слоев.

Примером системы, осуществляющей преобразование в растровый формат, может служить продукт фирмы ESRI ArcPress. Это программный растеризатор, преобразующий векторную, pастровую или смешанную векторно-растровую графику в формат растрового устройства вывода, растр заданного разрешения и размера. Он обеспечивает быструю распечатку карт и изображений на растровых устройствах вывода, таких, как струйные и электростатические плоттеры.

В качестве входных данных он может использовать как графические метафайлы в стандартах ESRI, так и файлы других систем в форматах CGM, PostScript (Level 1, Level 2). На выходе ArcPress могут быть получены растровые форматы для направления на устройство вывода и для экспорта в другие форматы, использующиеся для обмена (TIFF, РВМ, РСХ, BW, BMP, ВIТ).

ArcPress выполняет программную растеризацию непосредственно на рабочей станции, используя ее ресурсы памяти. Это позволяет обойтись без добавления памяти в плоттер стандартной конфигурации (особенно при выводе на большие форматы), одновременно распечатывать один файл и растеризовать другие, исключить ограничения на размер файла для устройства вывода.

5.3.3.Проекции и проекционные преобразования

Координаты точек пространственных объектов используют для указания местоположения объектов на земной поверхности. Поверхность Земли имеет сложную форму. При составлении карт пространственное положение точек отображается в плоском (двухмерном) представлении, Для отображения положения точек поверхности на плоскости применяют различные математические модели поверхности, задающие различные картографические проекции.

Группа математических процедур ГИС, осуществляющая переход от одной картографической проекции к другой или от пространственной системы к картографической проекции, носит название проекциоиных преобразований. Эта группа реализуется методами моделирования, образуя единый блок. В этот блок входят и различные процедуры обработки пространственных данных для получения новых проекций на основе исходных. Эти процедуры включают и простые операции пересчета координат пространственных объектов (поворота, смещения, масштабирования и т. п.), более сложные (связанные, например, с "укладкой" объектов в систему опорных точек) и самую сложную подгруппу операций (трансформация картографических проекций).

Число проекционных преобразований в блоках моделирования ГИС различно: в системе ER Mapper их свыше 700, в ГеоГраф — около трех десятков, а в некоторых настольных системах (DeskTop GIS) их нет вообще.

Рассмотрим наиболее общие классы проекционных преобразований [2] для решения задач в ГИС.

Преобразования картографических проекций применяют для перехода от исходной (хранимой в базе данных) картографической композиции к задаваемой пользователем. В частности, когда цифровая карта (слой), выполненная в известной проекции и соответствующая ее теоретическим координатам, должна быть преобразована в географические координаты либо в другую картографическую проекцию.

Достоинством моделирования в ГИС является возможность трансформирования космического (или аэро-) снимка непосредственно в картографическую проекцию, минуя построение фотограмметрической модели или традиционное фотограмметричесюе трансформирование снимков. Эта возможность предоставляется в пакетах ГИС, в первую очередь связанных с обработкой данных дистанционного зондирования.

Выделение подгруппы преобразования проекций связано с необходимостью интеграции данных из различных картографических источников с разнородной математической основой. Карты могут отличаться моделью Земли, примененной при создании карты; картографической проекцией; системой координат, привязанной к используемой модели Земли.

Технологически для проекционных преобразований в ГИС необходимо создать файл описания картографической проекции и выбрать исходный файл. Из набора типов преобразований выбирают необходимое, задают требуемые параметры, и проекционное преобразование осуществляется автоматически путем создания новой картографической проекции в заданном слое и соответствующем файле.

Проекционные преобразования требуют рассмотрения различных классов проекций, применяемых для создания карт[2]. Картографические проекции классифицируют по различным признакам, например в зависимости от характера и размера искажений.

Равноугольные проекции (conformal projection) сохраняют без искажений утлы и формы малых объектов, но в них резко деформируются длины и площади объектов. В математике такие преобразования называют конформными.

Равновеликие проекции (equivalente projection) не искажают площадей, но в них искажены углы и формы объектов. Первый вид проекций приемлем для прокладки маршрутов транспортных средств, второй для определения площадей и землепользования.

Произвольные проекции (arbitrary projection) имеют искажения углов, площадей и длин, но эти искажения распределены по карте, например, так, что минимальные искажения имеются в центральной части и возрастают к краям. Среди произвольных проекций выделяют равнопромежуточные (equidistant projection), в которых искажения длин отсутствуют по одному из направлений: вдоль меридиана или вдоль параллели.

Конические проекции (konical projection). По характеру искажений конические проекции могут быть различными. Наибольшее распространение получили равноугольные и равнопромежуточные проекции.

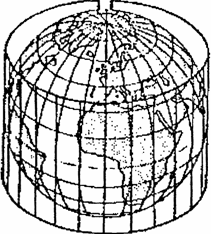
Образование конических проекций можно представить как проектирование земной поверхности на боковую поверхность конуса, определенным образом ориентированного относительно земного шара (эллипсоида) (рис. 5.1, а). В прямых конических проекциях оси земного шара и конуса совпадают. При этом конус берется или касательный, или секущий.

После проектирования боковая поверхность конуса разрезается по одной из образующих и развертывается в плоскость (рис. 5.1, б). При проектировании по методу линейной перспективы получаются перспективные конические проекции, обладающие только промежуточными свойствами по характеру искажений.

Другой метод образования конических проекций — аналитический. В его основу положены уравнения проекций, вытекающие из их определения и формулы общей теории искажений. В конических проекциях имеются две постоянные проекции а и с, Постоянная а равняется синусу широты стандартной параллели или, что то же самое, синусу угла при вершине конуса.

В зависимости от размеров изображаемой территории в конических проекциях принимаются одна или две параллели, вдоль которых сохраняются длины без искажений. Одна параллель (касательная) принимается при небольшом протяжении по широте; две параллели (секущие)— при большом протяжении для уменьшения уклонений масштабов от единицы. В литературе их называют стандартными параллелями.

Коническая проекция данной группы вполне определяется, если заданы постоянные проекции или любые величины, с ними связанные. Это могут быть широты стандартных или крайних параллелей. В последнем случае, например, может быть дополнено условие, чтобы масштабы на крайних параллелях и на параллели с наименьшим масштабом были равны по абсолютной величине.

Азимутальные проекции (azimuthal projection). В них параллели (альмукантараты) изображаются концентрическими окружностями, а меридианы (вертикалы) — пучком прямых, исходящих из центра (рис. 5.2, а).

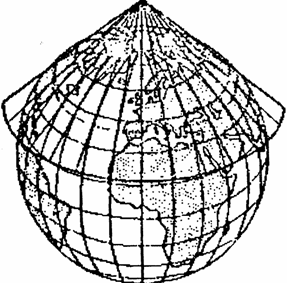
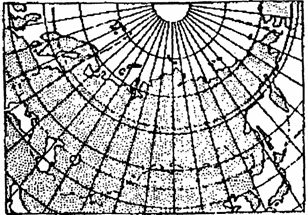
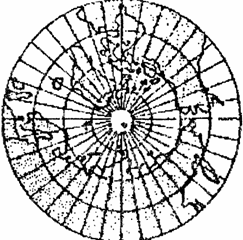
Рис. 5.1. Коническая проекция: принцип построения проекции; б — вид проекции

Рис. 5„2. Азимутальная проекция: а — принцип построения проекции; б — вид проекции

Углы между меридианами проекции равны соответствующим разностям долгот. Промежутки между параллелями определяются принятым характером изображения (равноугольным или другим) или способом проектирования точек земной поверхности на картинную плоскость.

Нормальная сетка азимутальных проекций ортогональна. Их можно рассматривать как частный случай конических проекций, в которых a = 1

Применяются прямые, косые и поперечные азимутальные проекции, что определяется широтой центральной точки проекции, выбор которой зависит от расположения территории. Меридианы и параллели в косых и поперечных проекциях изображаются кривыми линиями, за исключением среднего меридиана, на котором находится центральная точка проекции. В поперечных проекциях прямой изображается также экватор: он является второй осью симметрии.

В зависимости от искажений азимутальные проекции подразделяются на равноугольные, равновеликие и с промежуточными свойствами.Впроекции масштаб длин может сохраняться в точке или вдоль одной из параллелей (вдоль альмукантарата). В первом случае предполагается касательная картинная плоскость, во втором — секущая. В прямых проекциях формулы даются для поверхности эллипсоида или шара (в зависимости от масштаба карт), в косых и поперечных — только для поверхности шара (рис.5.2, 6).

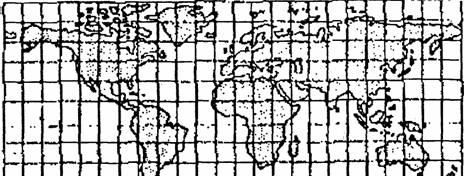
Цилиндрические проекции (cylindrical projection). В прямых цилиндрических проекциях параллели и меридианы изображаются двумя семействами параллельных прямых линий, перпендикулярных друг другу. Таким образом задается прямоугольная сетка цилиндрических проекций (рис. 5.3, а),

Промежутки между параллелями пропорциональны разностям долгот. Промежутки между меридианами определяются принятым характером изображения или способом проектирования точек земной поверхности на боковую поверхность цилиндра. Из определения проекций следует, что их сетка меридианов и параллелей ортогональна. Цилиндрические проекции можно рассматривать как частный случай конических при а=О (вершина конуса в бесконечности).

По свойствам изображения проекции могут быть равноугольными, равновеликими и произвольными. Применяются прямые, косые и поперечные цилиндрические проекции в зависимости от расположения изображаемой области. В косых и поперечных проекциях меридианы и параллели изображаются различными кривыми, но средний меридиан проекции, на котором располагается полюс косой системы, всегда прямой.

Рис. 5.3. Цилиндрическая проекция: а — принцип построения проекции;

Дата добавления: 2014-01-20