Вольт-амперные характеристики низкоразмерных структур

Электроны в структуре с размерами меньшими, чем длина когерентности электронной волны, фактически распределены по всему ее объему. По этой причине электрические свойства такой структуры пространственно неоднородны. Кроме того, из-за волновой природы электрона на перенос носителей заряда в ней оказывают влияние процессы, происходящие за ее пределами. Это влияние передается в структуру через контакты, которые следует рассматривать как составную часть самой структуры. Транспортные явления в низкоразмерных структурах и соответствующих электронных устройствах непосредственно связаны с интерференцией многократно рассеянных электронных волн. Их нельзя описать обычными моделями транспорта носителей заряда в твердом теле, основанными на уравнении Больцмана. Они требуют такого подхода, в котором квантовая когерентность может быть включена в модель. Адекватный подход был предложен Бютикером на основе более ранних работ Ландауэра.

В рамках формализма Ландауэра–Бютикера (Landauer – Buttiker formalism) перенос носителей заряда в низкоразмерных структурах рассматривается с позиции прошедших и отраженных электронных волн. С этой точки зрения проводимость определяется количеством одномерных каналов, доступных для носителей заряда, инжектированных из контактов с разупорядочением фазы – контактов, допускающих прохождение электронных волн с произвольными фазами. Это схематически проиллюстрировано с помощью многовыводного устройства на рис. 10.4, представляющего собой низкоразмерную структуру, соединенную с i независимыми источниками электронов.

Рис. 10.4. Многовыводное устройство, представляющее собой низкоразмерную структуру, соединенную с i независимыми источниками электронов.

Каждый источник характеризуется некоторым химическим потенциалом µ_i. Поток электронов, инжектируемых из i-го источника, равен

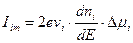(1.2)

Здесь e – заряд электрона; v_i – скорость электронов; dn_i/dE – плотность электронных состояний в проводящем канале;

∆µ_i =µ₁ – µ₀, где µ₀ – самый низкий химический потенциал в одном из подключенных источников электронов. Множитель 2 учитывает спиновое вырождение электронов.

Для одномерной структуры, то есть для квантового шнура,

(1.3)

где h – постоянная Планка.

Таким образом, ток, инжектируемый источником в i-канал, равен

(1.4)

Не все инжектированные электроны поступают в рассматриваемую структуру. Часть их отражается и возвращается обратно в источник, что описывается соответствующим коэффициентом отражения R_i в каждом из подводящих каналов. Электрический ток, протекающий по i-му каналу, уменьшается также и за счет электронов, переданных в него из других каналов, что описывается коэффициентом передачи T_ij из j-го в i-й канал. С учетом этого результирующий ток в i-м канале составляет

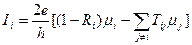(1.5)

Если теперь предположить, что каждый подводящий канал является многомодовым, то есть в нем имеется N_i занятых электронами подзон, более общее выражение для тока в нем запишется в виде

(1.6)

Отметим, что µ_i = eV_i, где V_i – напряжение, прикладываемое к i-му каналу. Предполагается, что источники насыщают электронами все каналы одинаково до соответствующей энергии Ферми в данном канале. Электроны, отраженные и переданные в различных m и n модах, должны быть учтены суммированием:

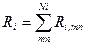, (1.7)

Здесь R_i включает все электроны моды m, отраженные в моде n. Аналогично и для T_ij. В обоих случаях суммирование проводится по всем m и n. Сохранение полного тока, инжектированного из i-го канала с учетом токов, которые покидают устройство через другие каналы, приводит к тому, что правило сложения для коэффициентов отражения и пропускания имеет вид

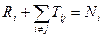(1.8)

Уравнение (1.6) является формулой Ландауэра–Бютикера для проводимости устройства с множеством выводов. Во многих отношениях оно может быть названо законом Ома для низкоразмерных структур. Эта формула полезна при качественном объяснении множества экспериментальных наблюдений. Она неплохо работает при описании открытых структур, в которых распространяются невзаимодействующие электронные волны, а взаимодействия вносят вклад только через конечное смещение фаз во времени. В закрытых квантовых точках, где важна энергия носителей заряда, она обычно не работает, исключая специальные случаи.

При температурах, отличных от нуля, квантование проводимости удается обнаруживать до тех пор, пока величина тепловой энергии k_BT не станет сопоставима с энергетическим зазором между ближайшими модами. Для того чтобы расширить область применения многоканальной формулы на температуры, отличные от нуля, должна быть принята во внимание зависимость коэффициента передачи от температуры.

Моделирование переноса носителей заряда в реальных трехмерных системах требует применения более сложных подходов. Один из них основан на использовании функций Грина. При этом решаются соответствующие уравнения для одночастичной функции Грина. Знание функции Грина позволяет вычислить амплитуды передачи и отражения, которые составляют S-матрицу (матрицу рассеяния) системы и согласуются с представлениями о распространении электронных волн в рамках модели Ландауэра–Бютикера. Кроме того, функция Грина устанавливает непосредственную связь с другими моделями переноса носителей заряда, такими, как теория линейного отклика на основе формулы Кубо, которая в надлежащих пределах соответствует формализму Ландауэра–Бютикера. Следует отметить, что использование функций Грина при описании транспорта носителей заряда в наноразмерных структурах связана не только с тем, что они являются в вычислительном отношении менее обременительными, чем другие методы. Скорее это обусловлено тем, что они содержат обширную связь с первоначальными принципами теории переноса носителей заряда во взаимосвязанной иерархии теоретических моделей. В частности, включение различных взаимодействий типа рассеяния на фононах трактуется без затруднений. Описание подходов, основанных на использовании функций Грина, можно найти в специальной литературе.

Дата добавления: 2014-01-20