Энергия переменного электромагнитного поля. Вектор Умова-Пойнтинга

Лекция №11

Из курса физики известно, что энергии электростатического и магнитного полей в заданном объеме определяются такими формулами,

, .

Естественно, что в переменном электромагнитном поле, в котором присутствуют и электрическая и магнитная составляющие напряженностей и 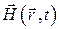, , полная энергия поля в объеме равна

.

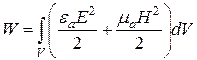Так как 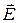и и являются функциями времени, то составляющая объемной плотности энергии электрической компоненты поля и составляющая 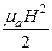магнитной компоненты также изменяются во времени. Во времени будет изменяться и полный запас энергии в объеме . Необходимо понять, что будет происходить с энергией в объеме с течением времени.

Запишем первые два уравнения Максвелла в таком виде

,

.

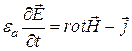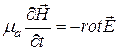Составим скалярное произведение первого уравнения с вектором 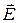, а второго – с вектором и просуммируем их. В результате получим

.

Так как

, ,

то левая часть уравнения (11.4) запишется в виде

.

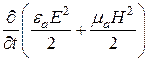Очевидно, что выражение (11.5) характеризует изменение во времени объемной плотности энергии.

Учитывая ранее полученную формулу (см.Л.8. (8.19))

,

первые два слагаемых в уравнении (11.4) запишем так

.

Тогда в целом уравнение (11.4) примет такой вид

.

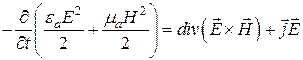После интегрирования (11.6) по объему получаем

,

где

.

W – энергия поля, запасенная в объеме ; 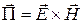– вектор, получивший название вектора Умова-Пойнтинга.

Слева в уравнении (11.7) выражение определяет скорость изменения во времени полной энергии в объеме . Его величина характеризует либо отток энергии из объема , либо приток энергии в этот объем в единицу времени. Если правая часть (11.7) – положительная величина, то . Это означает, что энергия в объеме убывает, т.е. имеет место отток энергии.

В соответствии с теоремой Гаусса-Остроградского первое слагаемое в (11.7)

.

Размерность этих величин равна размерности мощности. Поэтому следует ожидать, что – это поток мощности поля через поверхность 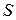, а – плотность этого потока.

Таким образом, вектор Умова-Пойнтинга

,

это плотность потока мощности или, что, то же самое, плотность потока энергии, проходящей через поверхность 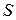за единицу времени. Это вектор, перпендикулярный векторам напряженности поле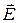й и . Направление этого потока соответствует правилу правого винта, вращающегося от 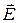к . Именно в этом направлении распространяется электромагнитное поле. И в этом же направлении осуществляется перенос его энергии. Второе слагаемое в (11.7) свидетельствует о том, что часть энергии поле расходует на разогрев объема . Величина этого расхода энергии в единицу времени равна мощности 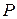(или количеству тепла , выделяемом в объеме в единицу времени), равными

.

В соответствии с (Л.5 (5.13)) эта величина также равна

.

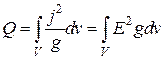Таким образом, уравнение (11.7) можно записать в следующем виде:

.

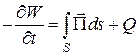Это уравнение было получено в 1885 году английским физиком Пойнтингом, а в общем виде, как понятие потока энергии – русским ученым Умовым Н.А. Соотношения (11.7, 11.13) являются содержанием теоремы Умова-Пойнтинга и характеризуют закон сохранения энергии.

Следует заметить, что величина потерь энергии на разогрев объема всегда является положительной величиной, т.е. .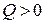

Поток может быть как положительным, так и отрицательным. Если 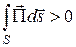, то энергия с течением времени в объеме убывает, т.е. выходит за пределы объема, рис. 11.1, 11.2. Очевидно, что в этом случае .

Если же , то энергия извне поступает в объем . Если при этом потери на тепло

,

то с течением времени энергия в объеме будет возрастать.

Рис. 11.1. Отток энергии из объема	Рис. 11.2. Приток энергии в объем

Приведем несколько примеров, иллюстрирующих процесс распространения энергии в соответствии с теоремой Умова-Пойнтинга.

1. Рассмотрим цилиндрический проводник радиуса и длины , вдоль которого течет ток , рис. 11.3.

Рис. 11.3. Цилиндрический проводник радиуса и длины ,
вдоль которого течет ток

Электрическое поле 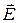вблизи проводника можно представить в виде векторной суммы нормальной 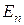и тангенциальной компонент. Вектор перпендикулярен линии тока. Следовательно, вектор Умова-Пойнтинга будет иметь две компоненты. Одна их них 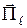направлена вдоль проводника, другая – перпендикулярно поверхности. Поэтому имеет смысл считать, сто с компонентой 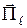связан перенос энергии вдоль проводника, а компонента поглощается проводником и связана с тепловыми потерями энергии в проводнике.

Эти потери нетрудно подсчитать

.

Плотность тока , следовательно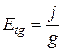. Для расчета величины у поверхности воспользуемся теоремой о циркуляции напряженности поля

,

где интеграл берется по окружности радиуса 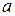непосредственно на поверхности проводника. Т.к. величина одинакова везде на этой окружности, то

.

Тогда

.

Подставляя величины и в формулу (11.14) получим, что

.

Т.к. плотность тока

,

а , то мощность

.

В соответствии с законом Джоуля-Ленца, эта мощность, определяемая потоком энергии внутрь проводника в единицу времени, расходуется на соответствующее выделение тепла.

2. Во втором примере рассмотрим, как передается энергия от источника ЭДС в нагрузку, характеризуемую сопротивлением , по обычным проводам, рис. 11.4. Ток полагаем постоянным, а сопротивление проводов равным нулю.

Направление передачи энергии, как видно из рис. 11.4, определяется вектором Умова-Пойнтинга . Видно, что направления тока в верхнем и в нижнем проводах противоположны. Однако передача энергии осуществляется в одном направлении – от источника ЭДС к нагрузке. И в верхнем и в нижнем проводах вектор направлен к нагрузке.

Необходимо отметить, что проводники являются лишь направляющими, вдоль которых канализируется энергия. Причем, наибольшая ее плотность имеет место, вблизи поверхности проводов. Энергия к нагрузке движется в среде вокруг проводников. В нагрузку также энергия поступает не из проводов, а из внешней среды. Символически это видно из направлений вектора вблизи нагрузки.

Рис. 11.4. Направление передачи энергии от источника ЭДС

Если провода имеют сопротивление, то возникает тангенциальная составляющая поля и появляется составляющая вектора направленная внутрь проводов, где поступающая в них энергия превращается в тепло.

Можно показать, что в коаксиальном кабеле, рис. 11.5, энергия передается не в проводниках, а в пространстве между ними. Причем основная часть энергии сконцентрирована вблизи поверхности внутреннего проводника.

Рис. 11.5. Коаксиальный кабель

Дата добавления: 2014-01-20