Граничные условия для электрической и магнитной компонент поля

Лекция №15

Как уже отмечалось, для получения единственного решения уравнений Максвелла в дифференциальной форме как уравнений в частных производных дополнительно необходимо знание граничных условий. Это связано с тем, что неизвестные функции в этих уравнениях представлены в виде их производных, подлежащих интегрированию. Операции же интегрирования дают неоднозначные результаты, которые конкретизируется введением начальных (во времени) и граничных (в пространстве) условий. Необходимость решения уравнений в дифференциальной форме (а не в интегральной) связана с тем, что именно уравнения в дифференциальной форме дают возможность найти поля в каждой конкретной точке исследуемого пространства с непрерывным изменением диэлектрической и магнитной проницаемостей. Граничные условия обычно определяют на границах, где заканчиваются непрерывные изменения этих параметров. Чаще всего это границы различных сред в пространстве, разделенных так называемыми поверхностями раздела. Такими поверхностями могут быть границы раздела сред: «воздух-почва», «воздух-металл», «воздух-диэлектрик», «металл-диэлектрик» и др.

Граничные условия обычно определяют с помощью уравнений Максвелла в интегральной форме для малых объемов пространства, стягивая их к бесконечно малым величинам путем предельных переходов.

Запишем систему уравнений Максвелла интегральной форме:

,

.

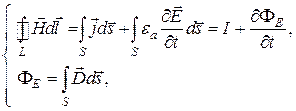
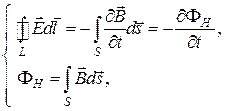
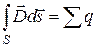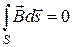Пусть имеются две среды, разделенные поверхностью раздела, которую в сравнительно малой области можно считать плоской. Среды различаются различными значениями электрофизических параметров 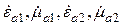, рис. 15.1.

Рис. 15.1. Граница раздела сред с параметрами

1. Найдем вначале граничные условия для нормальных компонент магнитного поля. Для этого точку 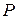поместим в бесконечно малый объем с площадью и высотой 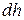, рис. 15.2, и вычислим поток вектора магнитной индукции (четвертое уравнение Максвелла) в пределе при .

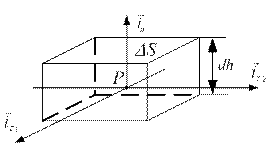
Рис. 15.2. К определению нормальных составляющих полей

.

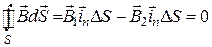Очевидно, что при 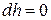поток через боковые грани равен нулю. Тогда

,

и нормальные компоненты вектора магнитной индукции 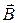в различных средах равны друг другу,

.

Так как , то

,

т.е. при переходе из одной среды в другую компоненты напряженности магнитного поля претерпевают скачок.

2. Найдем теперь граничные условия для нормальных составляющих электрического поля. Поступаем так же, как и при определении граничных условий для магнитного поля. В соответствии с теоремой Гаусса-Остроградского (третье уравнение Максвелла)

.

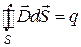Обратимся к рис. 15.2. Предположим вначале, что . Тогда, также как и для магнитного поля, для электрического поля получим,

,

т.е. нормальные компоненты вектора индукции электрического поля также равны друг другу, а компоненты напряженности электрического поля претерпевают скачок при переходе из одной среды в другую.

Если же на поверхности среды имеются заряды 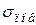, то

.

Тогда

.

В этом случае скачок претерпевают и значения вектора индукции.

3. Для нахождения тангенциальных составляющих магнитного поля на границе вычислим его циркуляцию по бесконечно малому контуру длиной и высоты 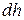(рис. 15.3), охватывающему точку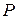(первое уравнение Максвелла).

Рис. 15.3. К определению тангенциальных составляющих полей

Учитывая, что при интеграл по этим поправлениям будет равен нулю, получим

.

Здесь возможны два случая.

В первом случае считаем, что проводимость среды конечна. Тогда при правая часть равенства также будет равна нулю и

,

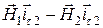или

,

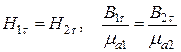т.е. тангенциальные компоненты напряженностей магнитных полей на границе равны нулю. Тангенциальные компоненты вектора магнитной индукции в этом случае претерпевают скачок.

Во втором случае считаем, что проводимость среды бесконечна (сопротивление равно нулю). В этом случае, как уже известно, ток потечет по поверхности в слое, в идеальном случае, нулевой толщины и

,

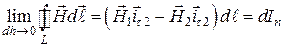или

,

где 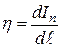– поверхностная плотность нормальной составляющей к площадке 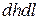тока (величина этой составляющей тока, приходящаяся на единицу элемента длины ).

Следует заметить, что внутри идеального проводника все составляющие поля равны нулю, т.е. 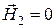. Тогда 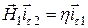. Ток течет в направлении перпендикулярном вектору .

В заключении рассмотрим граничные условия для электрических компонент электромагнитного поля. Для этого в соответствии с рис. 15.3 найдем циркуляцию по бесконечно малому контуру вектора электрического поля и учтем, что на боковых направлениях при 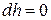интеграл по контуру будет равен нулю (второе уравнение Максвелла).

Тогда

.

Производная всегда является величиной конечной и при 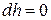правая часть этого равенства будет равна нулю, т.е.

,

.

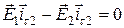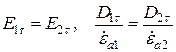Эти равенства свидетельствуют о непрерывности тангенциальных компонент напряженности электрического поля на границе раздела сред. В то же время значения соответствующих векторов индукции терпят разрыв.

В случае идеального проводника, как уже было рассмотрено ранее, все составляющие поля равны нулю. Т. к. 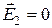, то

.

Это свидетельствует о том, что силовые линии электрического поля у поверхности идеального проводника перпендикулярны этой поверхности.

Дата добавления: 2014-01-20