Волновые уравнения и запаздывающие потенциалы

Основы теории излучения радиоволн. Волновые уравнения Даламбера и Гельмгольца.

Лекция №17

Излучение радиоволн имеет место в том случае, если в пространстве присутствуют токи, причем токи, имеющие составляющие ускорения. Эти токи часто называют сторонними. Они протекают, например, в антеннах под действием сторонних электродвижущих сил. Эти токи также могут возникать в проводящих средах, например, в ионосфере, под действием как собственных, так и сторонних полей. Задачу излучения можно решить, если решить уравнения Максвелла при заданных зарядах и токах, либо при заданных граничных условиях, образующихся наведенными токами или полями.

Запишем уравнения Максвелла:

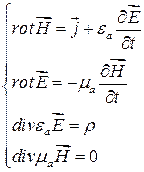. (17.1)

Применим операцию ротора к первому уравнению

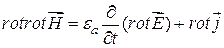. (17.2)

Подставим значение 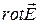из второго уравнения, тогда

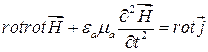. (17.3)

Ранее была выведена общая формула для двойной операции ротора

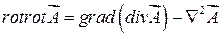. (17.4)

Т.к. 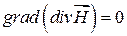в силу четвертого уравнения Максвелла, то имеем

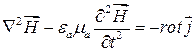. (17.5)

Выполняя аналогичные операции относительно второго уравнения Максвелла, получим

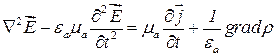. (17.6)

Эти уравнения называют волновыми неоднородными уравнениями или неоднородными уравнениями Даламбера.

Для свободного пространства, в котором отсутствуют токи 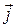и заряды 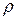, получим однородные волновые уравнения Даламбера.

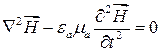, (17.7)

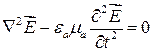. (17.8)

Эти равнения описывают распространяющиеся в свободном пространстве волновые поля. Решение этих уравнений заключается в нахождении 6-ти неизвестных – трех проекций вектора 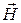и трех проекций вектора 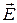. Для уменьшения числа неизвестных вводят дополнительно скалярные и векторные потенциалы, а также вектор Герца.

Векторный потенциал уже был введен для описания статического магнитного поля и позволил через понятие потенциала перейти к таким же описаниям магнитного поля, как и электрического.

Векторный потенциал определяется следующим образом:

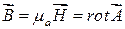. (17.9)

Тогда второе уравнение Максвелла запишется так:

,

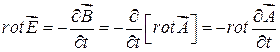или

.

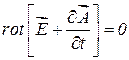Учитывая, что всегда

,

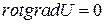можно записать по аналогии с формулами для расчета электрического поля по данным градиента потенциала:

,

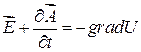или

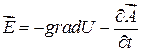. (17.10)

Используя такие связи полей со скалярным и векторным потенциалами, после несложных преобразований, аналогичным преобразованиям (17.2 - 17.4) получим неоднородные волновые уравнения Даламбера для потенциалов 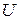и .

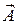, (17.11)

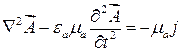. (17.12)

При отсутствии зарядов получим однородные волновые уравнения Даламбера:

, (17.13)

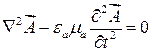. (17.14)

Заметим, что в отличие от уравнений (17.5-17.8), где нужно находить шесть неизвестных, при решении (17.11 - 17.14) необходимо найти лишь 4 неизвестных. Затем поля 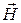и 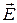следует рассчитать по формулам (17.9) и (17.10).

Часто вводят еще одну вспомогательную функцию 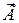, называемую вектором Герца. Эта функция определяется формулой:

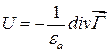. (17.15)

Можно показать (с помощью формулы Лоренца), что векторный потенциал

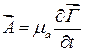, (17.16)

а вектор Герца находится из решения волнового уравнения Даламбера.

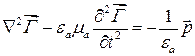, (17.17)

где 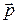- плотность вектора электрической поляризации (дипольный момент единицы объема - на самост. проработку).

Введение вектора Герца позволяет решить задачу относительно всего лишь трех неизвестных его проекций. Затем по известному вектору Герца с помощью формул (17.15, 17.16) можно найти потенциалы и 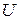, а затем и поля 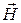и .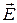

Для гармонических колебаний, представим в виде

, ,

, ,

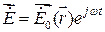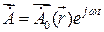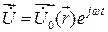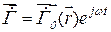
В результате их двойного дифференцирования по времени, например

.

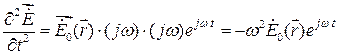При подстановке вторых производны в волновые уравнения Даламбера, получим уравнения Гельмгольца.

Например, для уравнения Даламбера (17.12) получим уравнение Гельмгольца для полей и их комплексных амплитуд соответственно:

, (17.18)

где 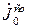- комплексная амплитуда плотности сторонних токов, создаваемых, например, антенной. Сторонние токи могут иметь место в ионизированных средах в результате воздействия на них сторонних электромагнитных полей.

Здесь учтено, что при переходе к комплексному представлению поля

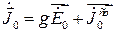, (17.19)

и проводимость 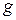включена в комплексную диэлектрическую проницаемость.

Аналогичные уравнения Гельмгольца имеют место для гармонических колебаний электрических, магнитных полей, скалярного потенциала и вектора Герца.

Для свободного пространства уравнения Гельмгольца, полученные из уравнении Даламбера, например, (17.8) для напряженности электрического поля будет иметь такой вид:

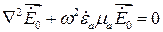. (17.20)

Учитывая, что скорость распространения электромагнитных волн в среде 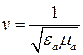, получим 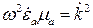, где 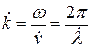– волновое число. Тогда уравнение Гельмгольца можно записать в таком виде:

.

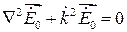В общем виде волновые уравнения Даламбера можно записать так

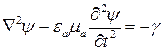, (17.21)

где

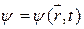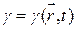, . (17.22)

Волновые уравнения Гельмгольца в общем виде будут иметь такой вид:

.

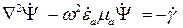
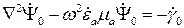Функциями 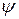могут быть , .

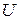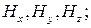
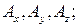
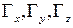Правая часть 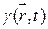, в зависимости от того, относительно какой функции решается уравнение Даламбера (E, H, A, U или Г) определяется зарядами и токами, существующими в объеме V, рис. 17.1.

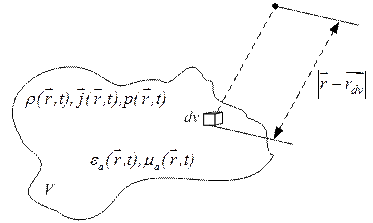
Рис.17.1. Исследуемый объем с зарядами и токами

В объеме V расположено множество элементарных объемов dV, каждый из которых можно считать точечным источником. Каждый точечный источник в исследуемой точке пространства 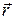и в некоторый момент времени t создает свое поле. Суммарное поле находится как сумма (интеграл по объему V) полей, создаваемых элементарными объемами dV. При этом нужно учитывать расстояние от каждого элементарного объема dV до исследуемой точки 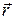и время запаздывания на распространения радиоволн от dV до точки .

,

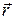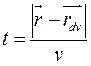где 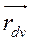– координаты объема dV.

Для элементарного источника dV волновое уравнение запишется в виде, аналогичном (17.21). Каждый точечный источник бесконечно малых размеров dV можно поместить в свое начало координат, вокруг которого пространство можно считать незаполненным зарядами и токами. Тогда уравнение Даламбера для такого источника dV можно записать в виде однородного волнового уравнения, справедливого везде, кроме начала координат:

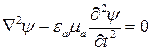. (17.23)

В сферической системе координат это уравнение имеет вид:

. (17.24)

Однако для точечного источника, в силу сферической симметрии, можно считать, что функция 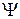зависит лишь от .

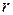Тогда волновое уравнение упростится и примет вид:

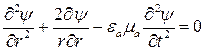. (17.25)

Введем переменную , .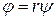

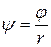В результате получим,

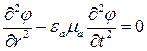. (17.26)

Проверим

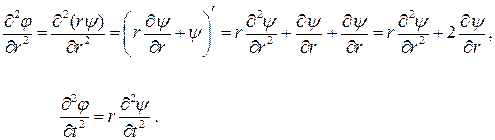
Или

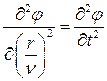, (17.27)

где 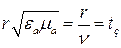, 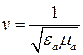– скорость распространения радиоволн.

Тогда уравнение (17.27) можно записать так:

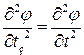. (17.28)

Такое уравнение уже было решено (см. Лекцию 13). Решениями будут волны:

.

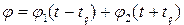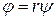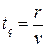Учитывая, что , а , получим, что

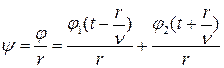. (17.29)

Это две сферические волны, одна из которых распространяется от начала координат.

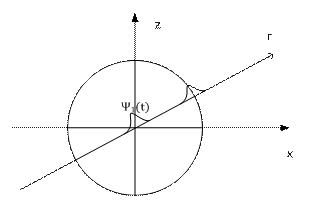
Рис.17.2.

Другая, с идет из бесконечности в начало координат (физического смысла не имеет). Поэтому имеет смысл рассматривать лишь одну волну.

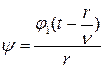. (17.30)

Прежде чем получить окончательные решения уравнений (17.11), (17.12), (17.17), вернемся к уравнениям, описывающим электростатические и магнитостатические поля. Так как в этом случае

, .

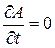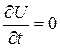То уравнения (17.11, 17.12) примут уже известный вид уравнений Пуассона, т.е.

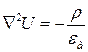, (17.31)

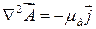. (17.32)

Очевидно, что заряды и токи в (17.31) и (17.32), отличие от (17.11), (17.12), являются постоянными величинами. Эти уравнения из уравнений Даламбера формально можно получить, если считать что скорость

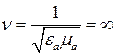, (17.33)

а

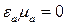. (17.34)

Раньше были приведены решения уравнений (17.31), (17.32). Для элемента объема dV, если его считать точечным элементом, решения (17.31), (17.32) имеют вид:

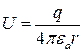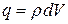, , (17.35)

. (17.36)

Суммарное решение определяется вкладами всех элементарных объемов, формируемых поля. Тогда

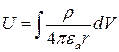, (17.37)

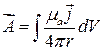. (17.38)

В общем виде уравнение Даламбера (17.21) для статических полей примет вид уравнения Пуассона

,

а его решение для точечного источника dV и источника с распределенной функцией 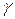(функцией координат) дает решение соответственно:

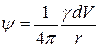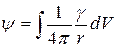, . (17.39)

Уравнение Даламбера при наличии правого слагаемого дает решение

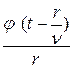, (17.40)

и можно считать, что для точечного источника

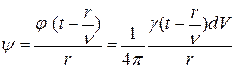, (17.41)

а для распределенного в объеме V

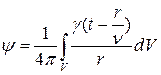. (17.42)

Тогда для скалярного 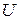, векторного потенциалов и вектора Герца имеем такие решения уравнения Даламбера

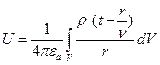, (17.43)

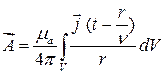, (17.44)

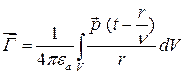. (17.45)

Потенциалы 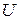и ,и вектор Герца называют запаздывающими потенциалами. Заметим, что если в уравнениях Даламбера принять условия (17.33, 17.34), т.е. , а 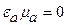, то приходим к уравнениям Пуассона (17.31, 17.32), а решения (17.43, 17.44) переходят в решения (17.37, 17.38).

Для гармонических колебаний выражения (17.43), (17.44), (17.45) находятся из соответствующих волновых уравнений Гельмгольца и соответственно равны:

, (17.46)

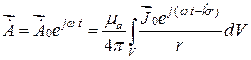, (17.47)

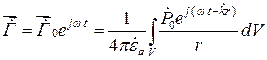. (17.48)

Дата добавления: 2014-01-20