Понятие о потоке вектора. Равенство Гаусса-Остроградского

Принцип суперпозиции полей

Для системы зарядов 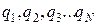суммарное поле будут равно

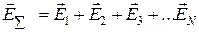
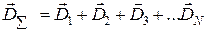, (1.6)

суммы здесь являются векторными.

В случае, когда N = 2, имеем следующую картину, рис. 1.4.

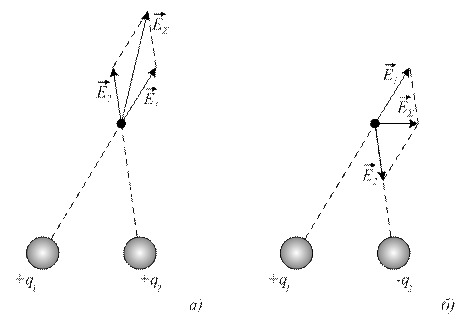
Рис. 1.4. Суммарное поле при взаимодействии двух зарядов: а) одного знака,
б) противоположных знаков

Подсчитаем суммарное "число" силовых линий, вектора электростатической индукции, прошедших через замкнутую сферу радиуса r, окружающую заряд q. Так как величина - это число силовых линий приходящихся на единицу перпендикулярной площадки, через которую эти линии проходят, то суммарное их число, прошедшее сферу будет равно

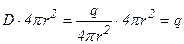. (1.7)

Таким образом общее число прошедших через всю сферу силовых линий, которое будем называть их потоком, равно величине заряда. Нетрудно показать, что это же число силовых линий пройдет через любую замкнутую поверхность, окружающую заряд q и будет равно величине q. Если же окружить замкнутой поверхностью несколько зарядов с суммарным зарядом 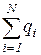, то суммарный поток через эту поверхность составит величину 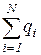. Это утверждение составляет основу равенства и теоремы Гаусса-Остроградкого.

Введем понятие потока вектора индукции следующим образом. Так как величина - это количество силовых линий, пронизывающих перпендикулярно к ним расположенную единичную площадку, то через площадку 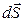произвольной ориентации пройдет такое число силовых линий

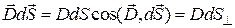. (1.8)

Это и есть поток вектора через площадку . Ориентацию площадки задаём вектором нормали , расположенным перпендикулярным этой площадке. Произведение 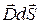является скалярным произведением векторов и . Площадь 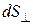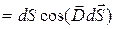расположена перпендикулярно потоку силовых линий вектора , рис. 1.5.

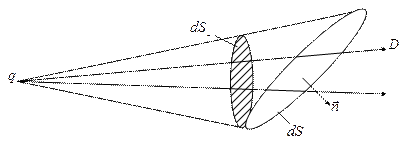
Рис. 1.5. Поток вектора 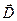через площадку

Общее число линий, проходящее через замкнутую поверхность S, окружающую заряд q, будет равно:

,

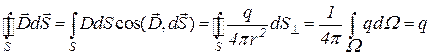где 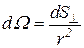- элемент телесного угла, а полный телесный угол при интегрировании составит 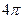. Нетрудно показать, что, если окружить замкнутой поверхностью N - зарядов с суммарным зарядом 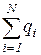, то

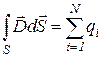. (1.9)

Это равенство составляет основу теоремы Гаусса-Остроградского и называется равенством Гаусса-Остроградского. Получено оно русским математиком Остроградским и независимо от него математиком Гауссом. Это равенство гласит, что поток вектора индукции через замкнутую поверхность S любого вида равно сумме зарядов, находящихся внутри объема, ограниченной этой поверхностью. Очевидно, что поток вектора через поверхность S в среде с диэлектрической проницаемостью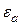

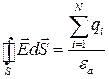. (1.10)

Дата добавления: 2014-01-20